The "Slim Jim" antenna has grown so popular among new radio amateurs who need a good antenna to work 2-meter repeaters that is has acquired its own name. Indeed, many newer amateurs think of the slim jim as a unique antenna, and some have claimed extraordinary performance capabilities for it--all without a good sense of what it takes to make such comparisons, of course. The seeming uniqueness of the antenna has even engendered some fairly poor explanations of how the antenna works. Therefore, it might be serviceable to spend a little time looking at the slim jim and seeing what may be its correct electrical origins.

In one sense, shown in Fig. 1, the slim jim is simply an alternative form of the common J-pole. The J-pole antenna itself is somewhat more complex in principle than it is to construct. It consists of an end-fed 1/2 wavelength radiator. Since the impedance of the radiator section is very high, we find a very old matching system consisting of a 1/4 wavelength section of transmission line. If we short the line at one end, it forms a transformer with a high impedance at the radiator end and a low impedance at the short. We may tap the line at some point above the short and obtain almost any impedance that we need for our transmission line. Today, a 50-Ohm tap is most common, but other impedance values are available. The exact tap point partly depends on the spacing between the matching section conductors and the conductor diameters, since the transformation of impedance along the line rests on the line's characteristic impedance.
One simple factor prevents us from holding the behavior of the J-pole to this straightforward explanation. The impedance at the top ends of the matching section lines is not equal, since one terminal is unconnected and the other sees a finite impedance at the radiator end. Therefore, the currents within the matching section are not equal in magnitude and opposite in phase. Rather, the currents are complex, having both radiating and transmission-line components. The existence of radiation currents within the matching section means that the entire J-pole structure radiates. The more widely spaced the matching section wires, the greater will be the distortion of the azimuth pattern from a true circle that we expect from vertical radiators, although the distortion does not rise to a level that ever disables the J-pole from effective omni-directional service. For additional information on basic J-pole configurations and operation, see the series at my web site called "Some J-Poles That I Have Known".
The slim-jim version of the J-pole arose after amateurs discovered that they could construct the antenna from a single length of common TV parallel transmission line or "ribbon" cable. Initially, builders cut one wire at the top of the matching section and stripped away the wire. Cheaper cables simplified the process, since we could get a plier-hold on the unwanted extra conductor length and pull it through the insulation. As a result, we still had the center insulation in which we could drill a hole and hang the antenna from the ceiling or some other convenient support. When not in use, we could wad up the antenna into a small ball for storage. These TV-lead J-poles have served any number of important purposes that have included getting a new amateur started on 2-meters, allowing bed-ridden amateurs to maintain communication with friends, and innumerable emergency services.
Amateur ingenuity mixed with amateur laziness eventually led to the discovery that we did not have to remove the second wire from the radiator. Instead, we could simply remove a small amount of wire at the top of the matching section and then connect the upper wire at the antenna top to form a continuous folded radiator section. For common TV lead-ins, we needed to reset the tapping point relative to the bottom short, but before long, the entire process became codified so that even the newest amateur could successfully built his or her own slim-jim version of the J-pole.
Enter the Zeppelin and the Quad
The J-pole antenna derives from the end-fed Zeppelin antenna that used to stream out behind the airships of the same name. The matching-section principles for feeding the high-impedance end of a wire were the same as used with the J-pole, even though the Zepp used the HF region for most of its communications. Today's end-fed Zepps as ground antenna installations sometimes use the same scheme of matching, although the matching section is at right angles to the antenna wire. This small tribute to historically significant antennas might end here, were it not somewhat mis-used in the case of the slim-jim J-pole design. The mis-use occurs as new users try to figure out why the slim-jim is "so good."

Fig. 2 shows the antenna that we typically think about as an end-fed Zepp: a 1/2 wavelength wire fitted with the 1/4 wavelength matching section. The end of any antenna shows a high impedance as the current goes to zero and the voltage climbs to very high levels. Hence, we may use the same 1/4 wavelength matching section with a wire that is 1 wavelength. Now, suppose that we fold the 1 wavelength back upon itself so that we still have 1 wavelength of wire but fitted into the space required by a half wavelength wire. Surely, some folks reason, we must obtain an advantage by having the long wire.
In fact, the fold-back wire provides no significant gain advantage over a single wire and may be the wrong model for understanding what a slim-jim J-pole may be. To understand the operating principles of the slim jim, we should turn to a different sort of antenna, the quad loop. A closed quad loop is a pair of dipoles in phase with each other, but it requires only a single feedpoint by virtue of the connection of the dipoles at the high-voltage, low-current points. The sketch of the closed quad at the upper left of Fig. 3 shows the general principle. The arrows indicate the current polarity at one instant in the life of the antenna. (Of course, the current direction shifts back and forth with radio frequency alternating current. However, by tradition, we use arrows to indicate the relative direction of current, using a time framework consisting of a single instant.)

The upper right portion of the figures shows a quad loop with a gap at the far right, that is, at one of the high-voltage, low-current points. If we place a small gap at such a point, we disturb the total continuity of the loop, but perfect continuity is not required for the loop to perform its task just as it would if we closed the loop. (Note: we can only create such a gap at the high-voltage, low-current point of the loop. If we create a gap at the point opposite the feedpoint--a high-current, low-voltage point--we shall change the loop's operation, that is, its pattern and its feedpoint impedance.) You may confirm this matter with any modeling software by comparing gapped and closed loops. As you widen the gap, you will need to adjust the element lengths necessary to sustain a resonant feedpoint. However, by moving in small steps, you will be able to convert named closed-loop antennas into named open-ended antennas, for example, changing a right-angle delta SCV into a half-square SCV.
The lower portion of the figure shows the application of the same principle to the antenna that we call the half wavelength folded dipole. On the left is a closed version, and on the right is a version with an opening at one end. In principle, the two antennas will show the same radiation characteristics. Both versions of the folded dipole provide both radiation and transmission-line currents that yield equal radiation performance and a 4:1 increasev in the feedpoint impedance relative to a linear dipole (assuming that both long elements use equal diameter materials). However, the pattern of transmission-line currents will not be the same for both folded dipoles. If we sort out those currents, the folded dipole's radiating currents prove to be virtually identical to the remaining radiation currents (the only currents) of a half wavelength single wire fed at its center.
If we feed the folded dipole at one of its closed ends, we may use the 1/4 wavelength matching system that we applied to the Zepp. Because we are feeding the antenna at the high-voltage, low-current position for each of its two wires, the impedance step-up ratio of a mid-element feed system becomes irrelevant to the antenna's operation. Under these conditions, we may have a gap at the far end of the antenna with no harm to the radiation characteristics. Equally, we may use the high-impedance feed system at the gap end of the antenna, connecting it to only one of the wires at the gap. Once more, the radiation characteristic will be unaffected by the feed system. This last condition is the slim-jim antenna.
Testing the J-poles Many Configurations
Let's put the account to a test. We may create many J-pole configurations, but we shall need only 5, the ones shown in Fig. 4. The first version is the standard J-pole with a single half wavelength wire as the radiator. (Because we are using a highly interactive radiator and matching system, the radiator of a J-pole is rarely a perfect half wavelength, even accounting for end effect, wire losses, and wire diameter.)

The second version of the J-pole is a pair of wires joined at the bottom of the radiator and the top of the matching section. We might expect the antenna to act like a single fat wire. The third form of the J-pole uses the typical slim-jim assembly of connecting the wire at the top but not at the bottom. The fourth in the series is almost gratuitous: a J-pole with a double wire, but with the second wire not attached at either the top or the bottom of the radiator section. The last model in the series makes connections at both the top and the bottom of the radiator section, thus creating an end-fed folded dipole.
All of the models use AWG #20 wire that is 0.032" in diameter. All parallel section of the antennas use a 0.375" spacing center-to-center. These dimensions partially simulate the typical slim-jim construction using typical TV lead-in. However, there are two important reservations, both of which involve the fact that TV lead-in uses vinyl insulation around and between wires. Since the matching section is a form of parallel feedline, its physical length will normally be the electrical length or the free-air length times the line's velocity factor (VF). For flat lines, a typical value for a TV lead VF is about 0.8. In the radiator section, the line is not acting as a transmission line, and so we must apply to it a different value for the VF, one more generally applicable to insulated wire elements. Values in the range between 0.95 to 0.98 are typical, depending on the insulation's conductivity and permittivity (or loss tangent).
In reaching a 50-Ohm impedance for all of the models, I limited the adjustments that I made to the model. All matching sections have the same total length from the line short to the top of the section: 22.5". I then adjusted the tapping point and the total height of the array. The latter adjustment is equivalent simply to adjusting the length of the radiator. For fine adjustment, I made small adjustments in the gap between the top of the matching section and the beginning of the second wire in parallel-wire radiators. However, the total range of these adjustments amount to 0.1".
With this much information on the model set-ups, we are ready to examine the data that emerged from the tests. Fig. 5 provides a guide to reading the dimensions listed in Table 1.

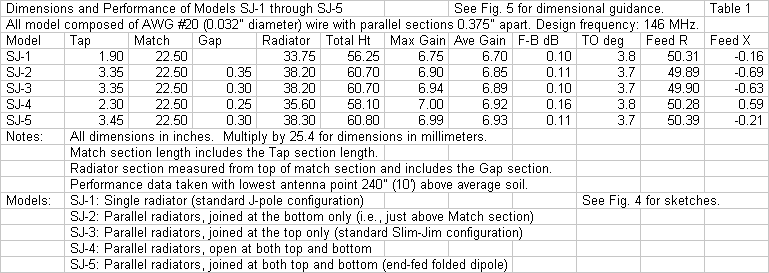
Dimensionally, models SJ-1 (single-wire radiator) and SJ-4 (double wire, no connection) are most alike. The single wire requires a tapping point closest to the matching section termination. It also uses the shortest radiator section that achieves resonance. Adding the second, unconnected wire moves the tapping point upward 0.4" and requires a 1.85" length addition to the radiator section. In fact, SJ-4's second wire acts like a closely and parasitically coupled independent wire. Although very close to the directly fed wire, the second wire creates the greatest front-to-back ratio of the collection of models. (The amount, of course, has only numerical interest and would not be operationally significant.) The operation of model SJ-4 strongly suggests that we need not have connected either end of the extra wire in the twinlead's radiator section when creating our J-pole. With the correct dimensions, the J-pole would have operated correctly.
The dimensional relationship among models SJ-2, SJ-3, and SJ-5 is striking. The folded-dipole version requires the longest radiator, at 38.3". Both versions that connect only one end use a radiator that is 38.2", regardless of the connected end. For all three models, the gap between the upper end of the matching section and the lower end of the second radiator wire varies by only 0.05". All three models require a tapping point that is considerably higher along the matching section. However, both gapped versions use the same tapping point, with the closed loop folded dipole only 0.1" higher.
All of the matching section have the same length, spacing, and wire size. Hence, all of them have the same characteristic impedance (Zo) (calculated at about 375 Ohms). The line Zo will be the geometric mean between the impedance at the end of the radiator and the shorted end. Since the shorted end--for all practical purposes--has a constant value that is near zero, the 50-Ohm position on the line will vary with the impedance at the radiator end. Subject to qualifications, the higher the radiator end impedance, the greater the impedance transformation down the line and hence the closer to the shorted end that we shall find the 50-Ohm point. Because radiation from the unbalanced termination will change the line currents relative to their values under perfect conditions, we can only use this basic relationship in broad terms, without precision calculation. However, the low tapping point of the single radiator (SJ-1) suggests that the radiator end shows the highest impedance of the model group. The unconnected second-wire model (SJ-4) moves the position upward a small amount, indicating that the presence of the second wire lowers the impedance at the end of the connected wire (where its end is the top of the matching section). All three of the connected double-wire models (SJ-2, SJ-3, and SJ-5) have a significantly higher tapping point, suggesting that their connections to the matching section exhibit significantly lower impedances. Of more than passing interest is the tight grouping formed by the three tapping points.
From Dimensions to Performance
Table 1 also provides modeled data on the performance of all of the J-pole models. The dimensions are simply the ones that yield the feedpoint impedance values (Feed R and Feed X) at a 50-Ohm level within +/-1 Ohm of that value and within +/-j1 Ohm of resonance. All antennas have the same base height of 20' (240") above average soil. The top height of the models varies by only 4.55" from the tallest to the shortest. Therefore, that difference makes no performance difference. All of the double-wire versions of the J-pole have maximum gain values that are within 0.08-dB of each other. The "strongest" of the group shows only a 0.23-dB gain advantage over the single-wire radiator (SJ-1), largely due to the effectively fatter radiators in the double wire versions. All TO angles are either 3.7 or 3.8 degrees. (All patterns taken of these models used an increment of 0.1 degrees in both the elevation and the azimuth patterns.)
The bottom line is that none of the models shows any operational advantage over any other model in the group. To demonstrate this point, we may overlay the patterns for the slim-jim version (SJ-3) and the folded-dipole version (SJ-5). Fig. 6 shows the result. I know of no way to separate the blue and black lines of the two plots.

As an incidental, note that the elevation pattern shows a depressed area about 15 degrees above the horizon. The anticipated lobe is not as strong as a smooth curve would yield and the nulls are not as deep as we might expect. This phenomenon is not a function of the antenna or its height above ground. Vertically polarized antennas exhibit this "depression" at the indicated angle over average ground, regardless of the antenna type or the height above ground. Over very good ground, the angle drops to about 12 degrees, and over very poor ground, the angle increases to about 25 degrees. Should the matter interest you, you may set a vertical antenna at perhaps 20 wavelengths above ground and take patterns using the 0.1-degree elevation increment. The high number of lobes and nulls that appear provides a much sharper indicator of the angle for the depression. Then you may systematically vary the ground conductivity and permittivity, treating each variable independently, and obtain some interesting curves. The exercise is electrically interesting but not operationally significant, since we normally are interested in point-to-point communications with vertical antennas at these frequencies.
The "depression" angle, of course, is the pseudo-Brewster angle (PBA) applied to vertically polarized antennas. Over dry land, where the conductivity is low, the angle is largely a function of the soil's permittivity. Therefore, we may simplify the calculation for general purposes to the following equation.

The equation omits the intermediate steps of defining a refractive index, which is the square root of the relative permittivity (or relative dielectric constant). At the PBA, we find neither additive nor subtractive effects from direct and reflected rays. Hence, we find neither a lobe or a null, and the gain is approximately the same as the free-space gain of the antenna. For further information on the pseudo-Brewster angle, see Chapter 3 of The ARRL Antenna Book, any recent edition.
Current Affairs
The data that we have developed should suffice to establish two ideas. First, since none of the J-pole configurations exhibits an operationally detectable difference relative to any of the others in the sampling range, the slim-jim configuration does not result in a superior J-pole. It simply results in a J-pole, and all properly constructed and matched J-poles are quite good antennas for FM repeater service. They are all free of significant horizontal dimension, since they need no radials to allow performance. Performance quality will largely depend upon the mounting height and the surrounding clutter that may interfere with paths to various targets.
Second, the tightness in the dimension groups among the models that make any connection to a second wire--as well as the performance similarities--should suffice to establish that the slim jim (SJ-3) and its bottom-connected brother (SJ-2) are forms of folded dipoles with a gap in one or the other end. However, one may wonder to what extent a folded dipole with a gap in one end at a high-voltage, low current point acts like a folded dipole, that is, as an antenna having both radiation and transmission-line currents. To satisfy myself on the matter, I examined the current profiles of the radiator sections of all of the models in the group. A graphic representation of the current magnitude distribution appears in Fig. 7.

All but one of the models yields a similar curve. Still, there are some pointers about reading the curves that may deserve attention. For example, with SJ-1, we have only a single radiator wire. Its curve is the continuation of the curve on the matching section wire to which it joins. Note that the current magnitude does not go to zero. The other side of the matching section that connects to nothing has a current curve that goes to zero, as indicated in the graphic by the current line touching the element line.
In SJ-2, we find that same matching section line with no connection going to zero. However, in this bottom-connected model, the connected matching-section line does not connect to either of the curves for the twin radiators. This situation is quite normal, since the current at the tip of the matching section is twice the value at the bottom of either radiator. That is, the radiator current has divided between the two branches, and each branch carries half the current at the junction point as the single line to which the radiators join.
For the slim-jim model (SJ-3), we show one radiator and one matching-section line with currents that go to zero. These are the unconnected ends. Like the other models, the current magnitude does not go to zero in the continuous wire as it passes the matching-section-to-radiator boundary. In fact, this region is not a boundary except as we need to set construction details. Electrically, it is more of a frontier between the radiating and matching functions.
SJ-4, of course, shows the current on both radiators going to zero at the top of the radiator section. At the matching-section end, the second wire current goes to zero, while the connected wire shows the "frontier" effect. Like all of the other models up to this point, the radiator current distribution curves are well formed; that is, they show peak current roughly at the center of the radiator length, with minimum values at the extremes.
The radiator section of SJ-5, the end-fed folded dipole, appears to show a wholly aberrant set of current distribution curves. In the closed folded dipole, we have two sets of currents: the radiation currents and the transmission-line currents. (In fact, in all of the double-wire models, we find both type of currents. However, the transmission-line components are generally too small to disturb the overall pattern of currents shown in the graphs.) Both current magnitudes are sufficiently high to affect the composite current magnitudes on each of the two wires. This result appears at face value to be in conflict with the radiation pattern reports, which show a completely normal set of results compared to the other models.
The resolution of the difficulty lies in sorting out the two types of current. Radiation currents are in phase with each other and therefore add together to form the radiation pattern. Transmission-line currents have opposite phase angles at any given facing point along the double line. Therefore, relative to radiation, they subtract from each other. The following simplified equations express this situation for each wire (A and B) in the parallel line:
On wire 1 (IA), we may treat the total current as the sum of the radiation and the transmission-line current, while on wire 2 (IB), we may treat the current as the difference between the transmission line and radiation currents. If we combine these basic relationships, we can calculate the net radiation current (IR) and the net transmission-line current (IT) for the pair of wires forming the folded dipole:
The information that modeling software (in this case, NEC-4) gives us is the current for each wire at facing points, which translate into segment numbers along the relevant wires. We can use this data to calculate the net radiating and transmission-line current values for each segment. The process, of course, is more involved than the basic equations reveal, since we must account for both the current magnitude and phase angle. (The full NEC output file will provide the current values both in terms of real and imaginary parts and in terms of magnitude and phase angle. We need the real and imaginary parts and can calculate them from the magnitude and phase angle if our software does not give us access to the component parts.) Once we perform the required work on the component parts, we must re-calculate final magnitude and phase values.
The radiator sections of all models used 14 segments. Table 2 shows the results of sorting the radiation from the transmission-line currents at corresponding points along the radiator of model SJ-5, where segment 1 is at the bottom and segment 14 is at the top.

The entry columns on the left show the values that produced the curves that we viewed in Fig. 7. What the curves did not show was the phase angle for each segment's current. The next most interesting facet of the table occurs in the phase-angle column of the transmission-line portion of the table. Note that the phase angle is almost the same for every entry. (The one seemingly aberrant entry of 18 degrees is a function of the magnitudes being too low to provide an accurate phase-angle calculation.) The relatively constant phase angle is a hallmark of transmission-line currents in folded dipoles. Had we used a center or current feedpoint for the folded dipole section, the value would have been about 90 degrees different than the source current phase angle. However, we do not use center feeding for a J-pole. For further notes on the current distribution in a folded dipole, see "Unfolding the Story of the Folded Dipole".

For our purposes, we need only sort the two currents and establish that the radiating current show a relatively normal pattern. Fig. 8 does this job by showing the magnitudes of the two types of current. With respect to the radiation pattern, only the curve for radiating currents is relevant, and its shape is completely normal. We find the maximum current value at about the center point of the radiator section, with values going toward zero at each and. Because the current values in a NEC calculation are taken at the virtual center point of a segment, their values never actually reach zero at element ends.
In fact, all of the models with double radiator wires, connected or not, show some transmission-line currents in the radiator section. Model SJ-2 had such currents from values of 0.007 to 0.068 at phase angles ranging from 22.1 to 22.8 degrees. Of course all current levels are relative to a source current magnitude of 1.0 at a 0-degree phase angle at the model source. Model SJ-3, the slim-jim version, shows transmission-line currents ranging from 0.003 to 0.10 at phase angles of 50 to 53.8 degrees. Even the unconnected model, SJ-4, shows magnitude values from 0.03 to 0.30 at phase angles of 79.9 to 82.3 degrees. In all three cases, the transmission-line current magnitudes are too small to appear in the distribution curves in Fig. 7 as more than a slight deviation from the curve of a pure radiation current distribution curve, such as the one shown for model SJ-1 with its single-wire radiator section.
Conclusion
The so-called slim-jim turns out not to be a special antenna, but only one of many ways to form a J-pole, an end-fed 1/2 wavelength radiator with a 1/4 wavelength matching section. Of course, that simple statement carries the qualification that the unequal impedance at the terminal ends of the matching section results in radiation from the matching section and complex interactions between the matching and radiating sections of the antenna. Whatever the form of the upper or radiating section, it remains a half wavelength fed at its end. So long as the section is a half wavelength, its performance will not vary significantly despite gyrations in the form.
Nevertheless, however obvious the conclusion may seem, the exercise has been useful in some respects. First, it has allowed the introduction of a more useful way of viewing the slim-jim configuration, that is, as a folded dipole with a gap at one of the high-voltage, low-current points. As well, the exercise has facilitated the analysis of complex currents in the folded dipole model to undergo analysis into their radiating and transmission-line components. Those exercises alone may well justify our original question into what the slim jim might be.
My junk box has just about enough twinlead to make perhaps 40 of these very useful 2-meter verticals, about 8 of each variety that we have discussed.
In the course of these notes, we over truncated some of the data presentation in order to progress along the lines of analysis in a reasonably efficient manner. We have a considerable amount of modeled and calculated data that may be of interest to those who may wish to probe more deeply into the J-pole with multiple wires in its radiator section or to examine more thoroughly the current distribution on a current-fed folded dipole. Therefore, I have added an Appendix for the data-hungry.
Updated 11-01-2006. © L. B. Cebik, W4RNL. This item appeared in AntenneX, October, 2006. Data may be used for personal purposes, but may not be reproduced for publication in print or any other medium without permission of the author.