
 Notes on a Wide-Band 50/75-Ohm Coax Feed System for Low HF Band Dipoles and Vees
Notes on a Wide-Band 50/75-Ohm Coax Feed System for Low HF Band Dipoles and VeesBack in 1997, Dave Leeson, W6NL, brought to my attention an interesting technique for achieving wide-band operation on the lower HF bands, especially the 80/75-meter band. The technique derived from mentions in texts and from references in ARRL publications by Frank Witt, AI1H, a noted experimenter and evaluator of low-HF broad-banding methods. Suppose that we have two desired operating frequencies, one in the 80-meter CW portion of the band and the other near the upper end of the 75-meter SSB portion of the band. A normal dipole would provide a single SWR minimum and would reach high values of SWR at the band edges. Alternatively, we might select one or the other end of the band and possibly use an antenna tuner to work the other band edge.

The broadbanding method begins by selecting the geometric mean between the two desired frequencies (that is, the square root of the product of the two frequencies). Suppose that we cut a dipole to be resonant at this frequency. Next, for the dipoles design frequency, we should cut a length of 50-Ohm coax that is a multiple of a half wavelength so that its length is perhaps from 0.5 wavelength to 2.0 wavelengths. Of course, the physical length will be the line's velocity factor times the electrical wavelength at the design frequency. To the shack or source end of this line, we connect a 1/4 wavelength 75-Ohm transformer line section, again multiplying the electrical length by the line's velocity factor to arrive at a physical length. Fig. 1 shows the general scheme.
The result is a well-establish broadening of the operating SWR-bandwidth. These notes are a bit of follow-up that seemed interesting as the numbers emerged from some modeling exercises. I used a dipole resonant at 3.75 MHz, ignoring the geometric mean part of the scheme, since I had no two special frequencies in mind. Actually, the scheme provides a certain wide-banding effect about whatever center frequency is chosen, and the available bandwidth is independent of any desired pair frequencies. My initial dipole was AWG #12 copper wires 128.8' long and fed at the exact center. My intention in 1997 was to provide a modeling demonstration that the technique was indeed feasible.
A decade ago, NEC software was limited to the calculation of transmission lines on a lossless basis. The most recent version of EZNEC has corrected this limitation and now allows the modeler to make use of lossy transmission lines by entering from convenient tables the loss per 100' (or meters) at the nearest frequency to the model's design frequency. I have interpreted the notion of "nearest frequency" to use a center line between tabular entries based on the geometric mean between entry frequencies. Therefore, in the following notes, we shall use the following cables and loss factors:
50 Ohms: RG-213, VF 0.66, Loss 0.6 dB/100' @ 10 MHz
75 Ohms: RG-216, VF 0.66, Loss 0.7 dB/100' @ 10 MHz
We shall proceed in 2 steps. First, we shall examine the general principles of the matching system using lossless cables, as I did in the last century. Second, we shall repeat the exercises using cables with real loss figures attached in order to see in what ways we may have to modify the conclusions drawn using only lossless lines. As a final step, we shall compare the results to Frank Witt's very interesting "Transmission Line Resonator" or TLR that he explained in detail in "Broadband Matching with the Transmission Line Resonator," The ARRL Antenna Compendium, Vol. 4 (1995), pp. 30-37. Since its initial publication, the TLR matching system has been a regular part of The ARRL Antenna Book, Chapter 9, where you will find an explanation and evaluation of a large collection of broadbanding systems. System evaluation includes not only how much of a band like 80/75 meters that we can cover with less than 2:1 SWR, but as well what losses we might incur due to our efforts.
1. Broadbanding a 3.75-MHz Dipole with Lossless Transmission Lines
Let's begin our journey by reviewing the properties of a 3.75-MHz AWG #12 resonant dipole at various heights above ground. We shall avoid the usual backyard 35' height, since that level is even below the height for maximum NVIS gain. Instead, we shall look at heights between 90' and 120' in 10' increments. One of the often-ignored features of horizontal antennas is that they change their feedpoint impedance as we change antenna heights, especially in the range from 1/4 wavelength to 1 wavelength. Table 1 provides some modeled data using average ground.
Table 1. Modeled performance of a 3.75-MHz 128.8' AWG #12 dipole over average ground Height Height Feed Impedance Max. Gain TO Angle feet wl R+/-jX Ohms dBi degrees 120 0.458 74.8 + j 0.0 7.30 31 110 0.419 82.5 + j 0.6 6.88 34 100 0.381 88.7 + j 4.2 6.51 37 90 0.343 93.1 + j10.6 6.24 41
The feedpoint impedance values are the modeled values taken at the antenna terminals and only at 3.75 MHz. In general, the resistance goes lower with a rising capacitive reactance below the design frequency. Above the design frequency, the antenna terminal impedance shows a higher resistance with a gradually rising inductive reactance. As the performance numbers show, the design-frequency impedance changes relatively rapidly even though the height range amounts to just over 0.1 wavelength. As well, in this height range, the gain and take-off angle (the elevation angle of maximum gain) also vary considerably.
The first order of business in broadbanding the antenna is to add 50-Ohm coax to the feedpoint in lengths from 0 to 2 wavelengths, using 1/2 wavelength increments. We shall initially omit the 1/4 wavelength 75-Ohm transformer, since the 50-Ohm lines have much to tell us on their own. We shall also keep the antenna at 120' above ground. With 5 different line lengths, let's take 50-Ohm SWR sweeps from 3.5 to 4.0 MHz in 0.05-MHz increments. The results will be the chart in Fig. 2 Only the last of the set of 5 lines shows clearly, since they overlay each other with perfection.

At first sight, it appears from the SWR that it does not matter how many half wavelength sections of 50-Ohm cable that we add. The results seem to be the same. However, that is the first illusion that we must overcome in understanding how the matching system works. When the line is lossless and used only at the frequency for which it is exactly 1/2 wavelength, then the source-end impedance (both the resistance and the reactance) are the same as at the antenna end of the line. However, when we move the operating frequency below 3.75 MHz, the operating wavelength is longer. Therefore the line becomes shorter relative to its length at 3.75 MHz. In this case, the different lengths of line will return different values of resistance and reactance, since the line is a different fraction of a wavelength in each case. Likewise, when we increase the operating frequency, the operating wavelength becomes shorter. The fixed line length then becomes longer than prescribed for the design frequency. Again, the different line lengths return different values of resistance and reactance.
The most general equation for calculating the impedance at the source end of a line for lossless lines is this one:


We may perform a similar exercise with respect to the reactive component of the source-end impedance. Fig. 4 shows the results. The curve for a single half wavelength section almost overlays the feedpoint curve. However, as we add more sections, the departure from that curve becomes far more extreme.

The resistance and reactance at each potential frequency and for each length of 50-Ohm line determine the load-end values for the 75-Ohm 1/4 wavelength impedance transformer. Ideally, for the transformer to function simply, the load-end impedance should be resistive and about 112.5 Ohms. Under these conditions, the transformer will show its source end value as 50 Ohms according to the standard simplified equation,

The matching system that we are exploring does not die from these conditions. In fact, these conditions are essential to making it work as a broadbanding system. When we combine the impedance range of 1/2 wavelength sections with the transformer, we obtain some possibly useful results. Fig. 5 presents the SWR curves for the complete system using lossless lines and 50-Ohm sections from 1/2 wavelength to 2.0 wavelengths.

With lossless lines, each curve has a potential use. For example, if we wish to have minimum SWR values at 3.65 and 3.85 MHz, a 2 wavelength section of 50-Ohm cable might be in order. However, the SWR values rise more rapidly beyond those frequencies than with a 1.5 wavelength 50-Ohm section. The line for a single 1/2 wavelength 50-Ohm section shows a single dip. Of the group, a 1 wavelength section of 50-Ohm cable provides the widest operating bandwidth: from below 3.55 MHz to above 3.95 MHz.
My dipole at 120' over level average ground had an independent feedpoint impedance of about of 75 Ohms. If we lower the antenna in 10' increments, we obtain the following data on approximate bandwidths between 2:1 50-Ohm SWR points. Despite the changes in the antenna terminal impedance values from one height to the next, Table 2 shows the matching system to be stable. At every height, curves for the various lengths of 50-Ohm cable remain congruent with the set shown for 120'.
Table 2. 50-Ohm 2:1 SWR bandwidth of a 3.75-MHz dipole at various heights
with various lengths of 50-Ohm cable in the broadband matching system
50-Ohm Length Lower limit Upper limit Bandwidth Lowest SWR
0.5wl 3.57 3.96 0.39 1.45
1.0 3.55 3.96 0.41 1.30
1.5 3.57 3.93 0.36 1.10
2.0 3.58 3.91 0.33 1.07
110' up" Z=82 Ohms
50-Ohm Length Lower limit Upper limit Bandwidth Lowest SWR
0.5wl 3.55 3.97 0.42 1.35
1.0 3.54 3.96 0.42 1.25
1.5 3.56 3.93 0.37 1.10
2.0 3.58 3.91 0.33 1.05
100' up" Z=89 Ohms
50-Ohm Length Lower limit Upper limit Bandwidth Lowest SWR
0.5wl 3.53 3.97 0.44 1.26
1.0 3.54 3.97 0.43 1.15
1.5 3.56 3.93 0.37 1.04
2.0 3.58 3.90 0.32 1.09
90' up" Z=93 Ohms
50-Ohm Length Lower limit Upper limit Bandwidth Lowest SWR
0.5wl 3.53 3.99 0.46 1.25
1.0 3.54 3.96 0.42 1.10
1.5 3.56 3.93 0.37 1.01
2.0 3.58 3.90 0.32 1.05
The graphs and tables so far go only as far as did the entire modeling analysis of 1997. The question remains open as to what sort of SWR curves we might obtain when using real coaxial cables, such as RG-213 and RG-216.
1. Broadbanding a 3.75-MHz Dipole with Lossy Transmission Lines
"Lossy" is a term that we apply to all real transmission lines. As such, it does not specify how much loss is involved, but only that more complex equations are necessary to calculate the source-end impedance for a given load impedance and factor in the real losses of the lines. The values for RG-213 and RG-216 come from the table on page 24-19 of the 20th Edition of The ARRL Antenna Book. There are lines with higher and lower losses than these relatively standard lines.
Let's replace the lossless lines in our initial models with these real lines and let NEC calculate the results. In both cases, the listed velocity factor of the lines is 0.66. Since a wavelength at 3.75 MHz is 262.286', the 1/4 wavelength section will be 65.572' * 0.66 or 43.277'. Each half wavelength of the 50-Ohm line will be 86.554' long.
We may now repeat the exercise by inserting into the model the physical length of the line, the velocity factor, and the 10-MHz loss factor for each of the two cables in the system. If we do this and run the model for each step shown in Fig. 5, we wind up with the set of 50-Ohm SWR curves shown in Fig. 6.

The cable losses do not significantly alter the curves for 50-Ohm sections that are 0.5 wavelength and 1.0 wavelength long. Both curves now provide complete coverage of the 80/75-meter band with SWR values of 2:1 or less. The more interesting results involve the use of 1.5 wavelength and 2.0 wavelength sections of 50-Ohm cable ahead of the 75-Ohm 1/4 wavelength transformer. The SWR minimums using the longest 50-Ohm section no longer reach the low values that we obtained for lossless cable. In addition, the minimum SWR values for a 1.5 wavelength 50-Ohm section move away from the center frequency on both sides of the center frequency.
One of the major reasons for the shift in the curves is the altered transformation of the feedpoint impedance along the now-lossy 50-Ohm cable sections. We may compare the results obtained with lossless cable in Fig. 2 with the results for lossy cables in Fig. 7. The top line shows the SWR curve for the antenna terminals themselves. Each lower line represents a 1/2 wavelength increase in the length of the 50-Ohm cable. With lossless lines, we could not separate the curves. With lossy lines, we can easily identify each curve, with the implication that at every point along each curve, the resistance and reactance values have also changed. When we combine the new impedance component values with the lossy transformer, the resulting SWR curves across the band also change their shape.

As we lower the height of the antenna and raise the pre-match feedpoint resistance, then lossy cables in the matching system show further variations from the lossless cable situation. Fig. 8 shows the curves for a height of 90' above average ground. The half wavelength and 1 wavelength 50-Ohm sections still provide the best band coverage. However, the double SWR minimum values are lowest with the 1 wavelength line. Both longer lines show a continued reduction in SWR bandwidth.

No broadband matching system is immune to losses. When we model lossy lines as a part of the model, the system losses show up as reduced maximum gain for the antenna. Most of the losses are a direct function of the matched cable losses plus a small multiplier due to the SWR value on each cable at each operating frequency. We may summarize the losses by checking the maximum antenna gain at the design frequency (3.75 MHz) and at the band edges. Table 3 presents the data, using the antenna itself with no matching system as a base line. The table is instructive, although it has limitations that we shall later note. The total line length value is the sum of the 50-Ohm and 75-Ohm cables used for each matching system variation. The loss value is relative to the antenna gain prior to adding the matching system.
Table 3. Maximum gain and TO angle of a 3.75-MHz dipole at 120' above average ground with variations of the 50-75-Ohm matching system
Total Line 3.5-MHz TO angle Loss 3.75-MHz TO angle Loss 4.0-MHz TO angle Loss
Length feet Gain dBi degrees dB Gain dBi degrees dB Gain dBi degrees dB
0 6.91 33 ---- 7.30 31 ---- 7.68 29 ----
129.83 5.67 33 -1.24 6.77 31 -0.56 6.61 29 -1.07
216.39 5.05 33 -1.86 6.43 31 -0.87 5.87 28 -1.81
302.94 4.46 33 -2.45 6.09 31 -1.21 5.21 28 -2.47
389.49 3.89 33 -3.02 5.76 31 -1.54 4.61 28 -3.01
(values for 220' of RG-213 50-Ohm cable)
4.92 35 -1.99 6.42 30 -0.88 5.77 30 -1.91
Since the cable has at the design frequency about a 0.45-dB loss per 100' when matched, the losses at 3.75-MHz show the approximate minimum loss obtainable from the cable under nearly matched conditions. However, at the band edges, we have seen sizable excursions in the feedpoint resistance and reactance, some above the 2:1 SWR values that we associate (rightly or wrongly) with good amateur equipment practice. The SWR value forms a (complex) multiplier on the basic cable loss, increasing the losses at the band edges.
We may repeat the exercise using a height of 90' above average ground to see whether the losses for each length of 50-Ohm cable remain consistent. Table 4 provides the results of this survey.
Table 4. Maximum gain and TO angle of a 3.75-MHz dipole at 90' above average ground with variations of the 50-75-Ohm matching system Total Line 3.5-MHz TO angle Loss 3.75-MHz TO angle Loss 4.0-MHz TO angle Loss Length feet Gain dBi degrees dB Gain dBi degrees dB Gain dBi degrees dB 0 6.10 44 ---- 6.24 41 ---- 6.44 39 ---- 129.83 5.07 45 -1.03 5.68 41 -0.56 5.36 39 -1.08 216.39 4.52 44 -1.58 5.31 41 -0.93 4.63 38 -1.81 302.94 4.00 45 -2.10 4.95 41 -1.29 3.98 39 -2.46 389.49 3.48 44 -2.62 4.59 41 -1.65 3.39 39 -3.05
Lowering the antenna height reduces losses at the lower end of the band, but the losses at mid-band and at the upper band edge remain relatively constant. The explanation is straightforward once we review Table 1. Without changing the length of the dipole element, the antenna is slightly long at 90', long enough to show up as a slight imbalance in band-edge losses.
The tables have one misleading aspect. They do not account for the actual cable length between the antenna and the actual transceiving equipment. Rather, they treat the antenna and any matching system as a unit. In practice, the serially linked cables would count as part of the cable run to the equipment. Only if the required cable run from the antenna to the equipment is shorter than the prescribed matching system will the matching system create additional losses. For example, if the required cable run is about 220', then the 1.5 wavelength and the 2.0 wavelength matching systems will create losses necessarily in excess of the losses in a simple cable run. The 0.5 wavelength and the 1.0 wavelength systems will create losses associated with the matching system plus the additional length needed to reach the equipment. Since these systems result in low SWR values across the band for a remaining 50-Ohm cable, these added losses will be limited to about the matched-loss value for the cable used. In this sense, the baseline gain values for the antenna are equally unrealistic, since they presume a perfect match at each frequency with a lossless cable. If we use our sample 220' length of RG-213, then the losses at the band edges will be higher if we employ no matching network at all. Table 3 has a special line of values for the antenna at 120' using 220' of RG-213 50-Ohm cable. Note that the loss values are not very different from those for the 1 wavelength matching system with a total cable length of 216'.
Lossy transmission lines used in the matching system may well alter our initial perceptions of the wide-band 50-75-Ohm matching system. Although lossless cables seemed to favor the longer system for some applications, the best lengths turn out to be either 0.5 wavelength or 1.0 wavelength of 50-Ohm cable prior to the 75-Ohm 1/4 wavelength transformer. Fig. 9 provides the outline of the system most favored by the use of cables with real losses. The system provides the widest coverage and the lowest losses possible.

The 50-75-Ohm matching system is simple and convenient. In most cases, we can tailor the version to match reasonably closely with the required cable run from the antenna to the shack. All connections are serial, with no hanging stubs or other appendages to add weight to the feedline. One remaining question is whether the system provides the greatest efficiency feasible.
The AI1H TLR Broadband Matching System
In 1995, Frank Witt, AI1H, presented an alternative to the 50-75-Ohm transmission-line broadband matching system. He called the system the Transmission-Line Resonator (TLR). It consisted of three lengths of 50-Ohm cable. We shall continue to use RG-213 with a velocity factor of 0.66 and a loss factor of 0.6 dB/100' as our implementation, which coincides with Witt's own version. A length of cable connects the antenna terminals to the source, which can be the station equipment or a further length of 50-Ohm cable that reaches the equipment. At the antenna terminals, he connects an open stub across the terminals, effectively adding a shunt capacitance (more correctly, a capacitive reactance) to the antenna terminal impedance. At the source end of what Witt calls the "link" line, he adds a shorted stub across the line, effectively adding a shunt inductance (or inductive reactance). With the proper proportions, shown for the 80/75-meter band in Fig. 10, the combination yields a broadband 50-Ohm match for the dipole.

The calculation details appear both in Witt's original article and in The ARRL Antenna Book. Our goal here is simply to model the Witt broadband TLR match and then to compare the results we obtain with the results we obtained from the 50/75-Ohm system that we have been examining. Witt requires a somewhat different length for his self-resonant dipole. He based his initial calculations on a frequency that was the geometric center of the band. However, as he refined the dimensions, he lowered the resonant dipole frequency from 3.742 MHz to 3.710 MHz. The model is based on a resonant dipole at Witt's frequency composed of AWG #12 copper wire at both 120' and 90' above average ground.
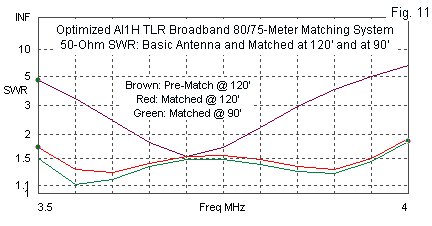
Fig. 11 shows the 50-Ohm SWR curves applicable to the model of the TLR system. The top line is the pre-match SWR curve, which reveals the minimum value that is below the center of the band. The next line down is the 50-Ohm SWR with Witt's dimensions for an antenna height of 120' above average ground. The lowest line is for the antenna at 90'. To optimize this curve, I reduce the source-end shorted-stub length from 20.1' down to 19'. Indeed, it appears that one can make fine adjustments to the TLR system simply by changing the length of the most convenient appendage to the link line, which for the modeled situation would be at or close to ground level.
The shape of the curve and its maximum and minimum values are very similar to those for the 50/75-Ohm series system when we use either a 0.5 wavelength or a 1.0 wavelength section of 50-Ohm cable. With respect to the SWR curves, the curves may show no advantage or disadvantage for each system. Structurally, the 50/75-Ohm system requires only serial connections of cables. The TLR system requires two appended stubs. The TLR physical length total 101' (ignoring the parallel-connected stubs), while the 50/75-Ohm system requires 130' of cabling for the 0.5 wavelength 50-Ohm section and 216' for the 1.0 wavelength section. Making a decision based on mechanical considerations would likely require consideration of the specific installation layout.
We may also compare losses in each system by using the data that the model provides for the two most eligible versions of the 50/75-Ohm system and the specified TLR systems. Table 5 shows the values at the band center and edges at both antenna heights. The lengths listed in the TLR entry include the stub lengths, which contribute to the overall loss picture.
Table 3. Maximum gain and TO angle of a 3.75-MHz dipole above average ground with variations of the 50-75-Ohm matching system and the TLR system Total Line 3.5-MHz TO angle Loss 3.75-MHz TO angle Loss 4.0-MHz TO angle Loss Length feet Gain dBi degrees dB Gain dBi degrees dB Gain dBi degrees dB Height = 120' 0 6.91 33 ---- 7.30 31 ---- 7.68 29 ---- 129.83 5.67 33 -1.24 6.77 31 -0.56 6.61 29 -1.07 216.39 5.05 33 -1.86 6.43 31 -0.87 5.87 28 -1.81 TLR (134.2) 5.51 33 -1.40 6.72 30 -0.58 6.41 29 -1.27 Height = 90' 0 6.10 44 ---- 6.24 41 ---- 6.44 39 ---- 129.83 5.07 45 -1.03 5.68 41 -0.56 5.36 39 -1.08 216.39 4.52 44 -1.58 5.31 41 -0.93 4.63 38 -1.81 TLR (133.1) 4.91 45 -1.19 5.58 41 -0.66 5.16 39 -1.28
At both heights, the losses are almost wholly dependent upon the line length and the degree of mismatch between the antenna terminals and the characteristic impedance of the line. With an intermediate length of transmission line between the two versions of the 50/75-Ohm system, the TLR shows intermediate loss levels. Indeed, one might suggest that for a broad but highly usable SWR characteristic, the 0.5 wavelength version of the 50/75-Ohm system is superior. However, certain types of equipment demand tighter SWR limits, for example, amplifiers with a 1.5:1 fold-back limitation. For such equipment, the TLR system offer the lowest losses possible.
Both the 50/75-Ohm and the TLR systems are adaptable to any frequency range in which a 13% operating bandwidth is required and the initial impedance is in the dipole range. As well both systems can be applicable to other antenna terminal impedance values by the proper selection of cables in the system. Our goal has only been to expand the initial modeling feasibility study to include loss factors, not to provide a generalized theory of cable matching. The range of available transmission-line characteristic impedances, of course, will always limit the 50/75-Ohm system.
Of course, if we are not confined to the use of coaxial cables, we may always attach a 450-Ohm parallel transmission line to the antenna and employ a well-balanced ATU in the shack. 220' of such line will have a loss of about 0.05-dB/100' (or about 0.11 dB for the total line length) in a matched condition on the band. The SWR values are not likely to incur great losses. Indeed, for the line itself, the losses will amount to between 0.3 and 0.4 dB across the band. However, the total system losses will depend upon the efficiency obtainable within the antenna tuner, and that value will change with the tuner design.
Updated 11-29-1997, 06-27-2007. © L. B. Cebik, W4RNL. Data may be used for personal purposes, but may not be reproduced for publication in print or any other medium without permission of the author.