My e-mail regularly contains a question that appears in various forms, but has one theme: Why have I not written anything about the gamma match? There are notes at my personal website on various forms of series matching systems and notes on the beta match. These two types of matching systems represent alternatives to the gamma match, especially when the task is to transform the generally low impedance of a Yagi array up to the value of 50 Ohms, as required by the most common feedlines used in amateur and other services.
Compared to a gamma match, series and beta matching systems are both simple and precise. Both systems make no alteration to the driven element, but add networks composed of transmission lines (usually) to the element feedpoint. The beta match does require that we initially set the driven element length to arrive at an optimal value of reactance relative to the feedpoint resistance, but the beta component is or is equivalent to adding a simple reactance across the feedpoint. The matching systems do not affect the radiation properties of the element.
As a consequence of these conditions, we may calculate the required values for series-matching or beta-matching components very precisely. In practice, the key factor affecting field adjustment of the systems is the accuracy of the velocity factor that we use in the calculations relative to the value that actually applies to the line used. If we know the velocity factor with measured accuracy (in contrast to the values we find in lists and specification sheets), we can often obtain the desired result with no need for further adjustment.
These fundamental matching systems are therefore amenable to automated formulation, that is, a utility program or a spreadsheet page that will tell us the required values if we input the feedpoint conditions and other values related to the components. In fact, I keep a spreadsheet on hand in my computer for just such calculations. It contains calculations for 1/4 wavelength matching sections, Bramham transformations, and Regier series matching calculations. In addition, it allows beta-match calculations and returns results for using either a shorted transmission-line stub or a solenoid inductor as the most common beta components. However, it also yields open lines and capacitance values should one choose to lengthen the driven element rather than shortening it. I have also added a page for the match-line and stub system of matching, used with higher-impedance antenna elements. I wrote the pages in Quattro Pro (.qpw), but have also saved them in Excel (.xls). You may download the sheet of your choice from the following addresses.
The Gamma Difference
The gamma match differs fundamentally from the other matching systems because it alters the physical properties of the driven element in ways indicated by Fig. 1. First, it adds new wires to the element, giving the element a more complex shape. Second, it changes the element feedpoint relative to the original element. The simple element uses a feedpoint position that normally is at the center of the element. The gamma-matched element places the feedpoint on a wire that joins the gamma rod to the main element.

One gamma-match advantage to many builders is the fact that the element may now connect directly to the boom. Both series and beta matching systems require driven elements that are insulated and isolated from any conductive support boom. In the era in which so-called "plumber's delight" construction methods ruled amateur Yagi construction, the gamma match equally ruled impedance transformation for coaxial feedlines. However, connecting the element to the boom changes its electrical length and therefore the feedpoint impedance prior to creating a gamma match. Therefore, most gamma match users began their calculations or experiments with only an estimated feedpoint impedance for the pre-matched element. NEC and MININEC antenna-modeling software offer no assistance here, since these programs only model axial currents (that is, along the element) and thus could not account directly for boom effects. Some builders have come to believe that a gamma match requires a direct connection between the boom and the element center. However, the connection is only an option, not a mandatory condition for the matching system.
One criticism of the gamma match accuses it of displacing the pattern in the direction of the match due to the size of the assembly. Effectively, as some believe, the assembly increases the diameter of the gamma side of the element, and this asymmetry of the driven element results in the main lobe's re-aiming. To test this notion, I constructed models of 28-MHz beams with identical reflectors and element spacing. One beam uses a simple driven element. The other uses a driver with the same overall length, but with a gamma match assembly (of course, with no boom). The gamma assembly is in the plane of the two elements and projects forward of the driver. The results of the test appear in Fig. 2.

The slightly lower forward gain of the gamma-matched version of the beam is an artifact of certain limitations of NEC (which we shall review shortly). The key factor in the overlaid patterns is the degree of lobe displacement, indicated by the lines that I added to the sides of the lobe. Displacement does indeed occur, but at a level too small for any user ever to notice in operation. The two patterns to the right show that the gamma match also has an affect on the free-space side nulls for the array. The simple beam has side nulls that show no limit. However, the gamma-matched beam has limited side nulls that are a mere 40-dB down from the level of maximum gain. I am unaware of any operational use of a beam in which one might be able to detect the difference.
The modeled test case assumes by its mathematical basis relatively perfect construction of the gamma-match driven element. I have in past years seen range-generated patterns for gamma-matched beams with a significant displacement of the main forward lobe. It would not be possible to perform a full analysis of such patterns without being able to model currents within the driven element and along the boom--if the elements makes a direct connection to the boom. However, in principle and assuming careful construction, pattern displacement is not a hindrance to the use of a gamma match.
Calculating the Gamma Match
H. H. Washburn, W3MTE, introduced the amateur community to the gamma match in his September, 1949, QST article, "The Gamma Match" (pp. 20-21, 102). D. J. Healey, W3PG, provided the first mathematical analysis of the match in "An Examination of the Gamma Match," QST, April, 1969 (pp.11-15, 57). Healy's treatment, however, required the use of nomographs and a Smith chart.
Since these seminal articles, several alternative analyses have appeared in amateur journals. H. F. Tolles, W7ITB, presented a purely mathematical analysis in "How to Design Gamma Matching Networks" in Ham Radio for May, 1973 (pp. 46-55). Because the Tolles equations proved tedious to many gamma designers, R. A. Nelson, WB0IKN, set them into a Basic program in "Basic Gamma Matching," Ham Radio, January, 1985 (pp. 29-33). ARRL converted Nelson's Apple-Basic program into a version suitable for IBM computers, and a listing appears in The ARRL Antenna Book, 16th Ed. (p. 26-20). In 2000, Dave Leeson, W6NL, corrected portions of the program so that it more accurately serves as a design vehicle to calculate gamma matches. This program is also available within the HamCalc collection of Basic utilities edited by George Murphy, VE3ERP. Fig. 3 shows the GW Basic listing for the version of the program distributed by ARRL.

Since the work of Tolles and Nelson, two alternative mathematical analyses have appeared. Ron Barker, G4JNH, presented "A New Look at the Gamma Match" in QEX, May/June, 1999 (pp. 23-31). Barker changes some of the fundamental assumptions about the key factors in a gamma match to arrive at his results. Unfortunately, his work is less amenable to easy placement in a Basic utility or a spreadsheet, since the calculations require the solution to simultaneous equations. In contrast, Roger Wheeler, G3MGW, returned to the Healey analysis and converted the graphical techniques back into mathematical methods that allow a straightforward spreadsheet set of calculations. Both of these later analyses rely on something that was unavailable to earlier gamma calculations. In most cases, the determination of the initial or pre-match driver feedpoint impedance rested on assumption, guesswork, or rudimentary measurement. Measurement became difficult if the builder connected the driver to the boom and did not allow for a feedpoint gap, even if it would later be closed. Both Barker and Wheeler require the use of antenna modeling software to determine the pre-match driver impedance. Other methods exist, for example, the Brian Beezley, K6STI, module in the overall program YO. However, Beazley has never published his procedures.
The downloadable spreadsheet contains pages for the Healey-Wheeler (HW) and the Tolles-Nelson-Leeson (TNL) methods of calculating gamma match rods and series capacitors. Every gamma-match calculating system tries to yield a physical value for the length of the gamma rod and a series capacitance value at the feedpoint to leave a pure resistive impedance. The required inputs appear in Fig. 4. We need to know the diameters of the main element in the region of the gamma assembly and of the proposed gamma rod, tube, or wire. As well, we must input the center-to-center spacing between the main element and the gamma rod. Ordinarily, the physical dimensions for the inputs and the outputs are in the same units of measure. The spreadsheets use inches.

In addition, we require two impedance values. One value is for the simple driven element, designated Ra and jXa in Fig. 4. We also need to specify a desired feedpoint impedance, Rf, which is the target resistive impedance that matches the main feedline. For our samples, we shall use 50 Ohms, since it is the most common value that we encounter in amateur radio applications. However, we may apply the gamma match for virtually any reasonable line impedance.
Fig. 4 also shows some of the points in the gamma assembly that exhibit derived impedances calculated somewhere within the system. Z1 is the transformed impedance based on the fact that the gamma assembly forms a shorted transmission line stub. (One misguided criticism of the Healey system was that it treats the gamma assembly as a folded dipole. Every folded dipole exhibits both radiation and transmission-line currents. In the calculation of the gamma line, we are concerned with the transmission-line performance of the assembly.) We can derive the characteristic impedance (Zo) of the stub using conventional equations that involve only the physical dimensions of the line. S is the center-to-center line spacing, and d1 and d2 are the diameters of the gamma rod and the main element, respectively.

The TNL system uses more fundamental equations involving havercosines. However, in the typical range of Zo (perhaps 200 to 600 Ohms), the differential in results between equations is less than 1% and normally only about 0.1%.
While we are using only the physical dimensions that we input to the calculation system, we can also calculate a step-up ratio between the original simple-driver impedance and the value shown as Z1 in Fig. 4. The most usually form of the equation again employs the three input physical values, S, d1, and d2.

Once more, the TNL system uses more fundamental equations, but the differential in result, compared to the more usual engineering formulation is well under 1%. Both the HW and TNL systems use this equation to calculate the value of Z1 (R1 +/- jX1) simply by multiplying Ra and jXa by the value of r. If the diameters of the main element and the gamma rod are the same, then r = 4. If the gamma rod is thinner than the main element, then r > 4. If the gamma rod is thicker than the main element (an unusual but possible situation), then r < 4 but r > 1.
We may add two side notes here. First, the Barker calculation system does not use the step-up ratio derived from the usual equation. Barker uses the impedance ratio between a simple driver element in isolation (essentially a dipole) to the impedance of the simple driver in service within the beam antenna. Second, at least the HW system does not account for the fact that the impedance undergoes not only a step-up in value, but also a shift in phase angle when we move from the driver without the gamma assembly to the driver with the assembly. If we model a gamma system and place the feedpoint at the position it would occupy on the pre-gamma driver element, we can observe the phase-angle shift in the impedance.
The HW system calculates the value of Z2, the impedance presumed to exist at the far end of the gamma assembly. If we assume that the current distribution is sinusoidal--which is close to correct but not precise--then we may use a standard equation to determine the values of R2 and X2.
Theta is the electrical length of a gamma assembly either in degrees or in radians at the design frequency. Since we cannot determine the value of theta without a physical gamma rod, the HW system calls for a trial length. In concert with the remaining calculations, we simply adjust the trial length until the value of Rf becomes 50 Ohms, if that is the target feedpoint impedance.
The TNL system operates differently. By addressing the required impedance and phase angle at the feedpoint, it calculates the required rod length using the factors already derived plus some ratios that appear in the listing in Fig. 3. The original Tolles article in Ham Radio provides the source of these ratios as they are applicable to the calculations. The Barker system uses neither of these methods, but creates an assumption of what must be the relative impedance at the gamma junction with the main element. He then calculates actual values from the initial driver impedance in a set of simultaneous equations.
The HW system derives the feedpoint impedance from two values in parallel. One value is the impedance of the gamma assembly as a shorted transmission-line stub having the length, theta, and the characteristic impedance Zo.
The other values are the values of Z2 as transformed by the same length of transmission line back to the new feedpoint. Wheeler follows Healey in using the following equation for this part of the impedance combination.

To resolve the equation, of course, one must break it into real and imaginary parts and then recombine them to arrive at the final value of Z3. (The TNL system essentially reverses the procedures and calculates the rod length from the required transformation.) We combine the parallel combination to arrive at an impedance that is the desired Rf in series with a value of Xf that is inductive. From this inductive reactance and the design frequency, we may determine the required series capacitance to leave us with a purely resistive feedpoint impedance.
I have tracked some of the rudimentary elements of gamma calculating systems to show what sort of thinking goes into them. However, the treatment is in no way complete, nor does it touch a number of the dimensions of the TNL and Barker systems. Instead, it is simply complete enough to allow one to track through the attached spreadsheet formulations of the HW and the TNL systems, in case one wishes to calculate a few typical gamma assemblies.
Testing the Gamma-Calculating Systems
Virtually all published gamma-calculating systems use one or two examples of the system's application and then declare the system adequate. Wheeler applied his formulation to gamma assemblies on quad loops. Tolles preferred VHF Yagis using gamma rods considerably thinner than the main element. Barker uses a single 20-meter beam as his test case. Of course, trying to develop a systematic set of test cases would be nearly impossible if we were restricted to constructing physical antennas having an interesting range of feedpoint impedance values for transformation.

It is possible to construct a series of antenna models to serve as a surrogate for the physical antennas. However, we cannot do the job in NEC-2 or even NEC-4. As suggested in Fig. 5, the gamma assembly presents NEC with two problems. First, unless the gamma and main elements are the same diameter, we encounter angular junctions of wires with dissimilar diameters. Although NEC-4 improves on the performance of NEC-2 under these circumstances, the results are insufficiently accurate for use as a comparator to the calculated values. In addition, gamma spacing is rather narrow for most beams that use relatively fat element diameters. Under these conditions, NEC tends to yield less than precise results. The relative unreliability appears in the average gain test (AGT) scores, which generally are no better than 0.92 when a perfect score would be 1.00. Since arriving at a feedpoint impedance of 50 Ohms is critical to the comparisons, AGT values in the range of 0.92 are too far from ideal to be useful. Values of 0.98 to about 1.02 are more valuable to the task of comparison.
Fortunately, MININEC is not sensitive to angular junctions of wires with differing diameters. However, in its raw form, it is subject to limitations related to close wire spacing and to angular junctions in general. One version of MININEC, Antenna Model, has introduced correctives that make it suitable for some first-order comparisons with the calculation systems. Note that I do not call the models "standards" against which we test the calculation systems. At best, the models are comparators so that we may observe some general trends as well as similarities and differences in outcomes.

Fig. 6 shows the general set-up for the modeling process. Although unnecessary for the pre-match model, I have assigned to each element the same number of segments used in the gamma model. The number of segments for each element derives from the test values of gamma spacing. All test models will use 28 MHz as the design frequency. The gamma spacing will use 4" as a center value and require 2 segments in the feedpoint wire to place the feedpoint at that wire's center. Hence, a 2" segment length becomes the standard. For some tests, we shall use gamma spacing values of 2" and 6", but the segment length differential will not prove too detrimental to the AGT scores. In fact, in the accumulated data, I shall show not only the modeled gamma rod length and the indicated series capacitor, but as well the AGT score to permit you to reach your own conclusion about the model's reliability.
From the very start, we recognize some important differences between the models and the calculation systems. Foremost among the differences is the fact that the models contain actual physical structures for the gamma far end shorting bar and for the feedpoint connecting assembly. In all models, I shall use end wires that have the same diameter as the main element, since in gamma assemblies applied to Yagis, the shorting bar and the coax connector plate tend to be substantial. Neither the HW not the TNL calculation system includes any allowance for such structures. Barker does add some fudge factors to his system, and the HW spreadsheet page includes an optional fudge-factor section at the end. The reason for the fudge factors is that calculations tend to call for capacitance values that are too high, and the models will reflect this fact by requiring lower capacitance values than the calculations indicate.
Test 1: A Simple Scaling Project
As an initial test, let's compare 3 perfectly scaled antennas with gamma matches. The test frequencies are 7, 14, and 28 MHz. For each frequency, I created a basic 2-element driver-reflector Yagi with a feedpoint impedance of 29.84 - j25.73 Ohms (typical of 0.12 wavelength element spacing). To ensure perfect scaling, the elements are lossless. (The calculation systems do not take material losses into account, and given the small size and generally large element surface areas used in beams, the losses would indeed be small.) The 10-meter antenna uses a 0.5" main element diameter, with a 0.375" gamma rod. The element-to-rod spacing is 4". All of these dimensions also scale upward as we lower the test frequency. Therefore, the 7-MHz version of the antenna uses a 2" main element, a 1.5" gamma rod, and 16" spacing. Even though the 40-meter dimensions may be somewhat larger than realistic, they will serve well in this test. The top section of Table 1 provides a more detailed run-down of the beam dimensions.
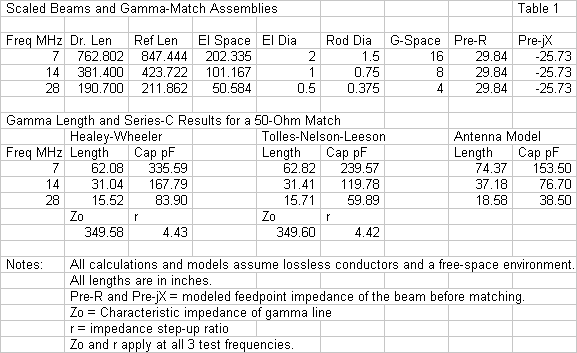
The lower portion of the table shows the calculated length of the gamma rod and the calculated series capacitance using the Healey-Wheeler and the Tolles-Nelson-Leeson system. It also shows the modeled values in the AM MININEC program. Because all dimensions are perfectly proportional, the calculated values of the gamma-line characteristic impedance, Zo, and the step-up-ratio, r, are the same for all three antennas. A review of the basic equations shown earlier will confirm this result.
As a consequence, we find that the two calculation systems also produce scaled values for both the gamma rod length and the required series capacitance. Likewise, the modeled gamma rod and series capacitance also internally scale within the limits that I set for modeling precision. I adjusted the rod length and the series capacitance until the feedpoint impedance reached 50 Ohms resistive, +/-0.1-Ohm, and j0 Ohms reactive, +/-j0.1 Ohm.
For this test case, the two calculating systems yield quite similar values for the gamma rod length. However, both values are 16-17% shy of the modeled value. One reason that I selected this initial test case was the fact that the calculation systems yield values smaller than the model. Theoretically, if we simply assume that the calculation system does not take the shorting bar into account, we would expect the calculated lengths to be slightly long. Hence, the systems and the model must have other differences.
As we expected from general gamma-match experience, both calculation systems over-estimate the required amount of series capacitance needed to bring the feedpoint impedance to a resistive 50-Ohm value. In this early test, we may also note that the two systems yield very different series capacitance values. Therefore, a single method of adding fudge factors into the determination of the final series capacitance value will not work for both systems.
However, I have to insert a reminder here. The modeled gamma match is only a comparator in this test (and in those yet to appear). It is not a standard against which to measure the adequacy of the two calculating systems. With the exception of the gamma-rod length, the 3 systems of determining the required gamma-rod length and the series capacitance merely yield different results.
Test 2: Changing the Ratios among Element Diameter, Rod Diameter, and Spacing
For a second test, let's modify the initial beam so that it is very close to resonant, with a feedpoint impedance of 32.07 - j0.05 Ohms. For this test, we may use a 28-MHz beam. Like the beam in the first test, the element spacing is 0.12 wavelength, so the only change is to the driver length. The main element diameters are 0.5". Once more, we shall explore the HW and TNL calculating system results and compare them with AM MININEC modeling results.
This test will be somewhat more complex. We shall explore 3 element-to-rod spacing values: 2", 4", and 6". As well, we shall look at gamma-rod diameters from 0.125" to 0.625" in 1/8" increments. A gamma rod that is fatter than the main element is unusual in reality, but certainly possible. Because we are changing both the diameter ratio between linear parts of the gamma assembly and the spacing between those parts, the values of both Zo and r will change with each sample case. The value of Zo will range from about 233 Ohms (for the 0.625" rod at a 2" spacing) to nearly 465 Ohms (for the 0.125" rod with a 6" spacing). The versions using 2" spacing will show the widest range of step-up ratio (r) values, running from about 3.6 for the fattest rod to 7.1 for the thinnest.
Table 2 catalogs the data for the series of tests. The top part of the table provides the initial antenna dimensions, along with the near-resonant pre-match feedpoint impedance. The next part of the table provides results for the three methods of determining the required gamma parameters. The AM section provides an additional column that lists the AGT score for each model in the set. The models using a 2" spacing are the farthest from ideal. It is not wholly clear that MININEC follows the same general AGT rules as does NEC. Hence, we cannot claim with assurance that the 50-Ohm impedance derived from the models (within the limits used in the first test) is off by no more than about 1.25 Ohms. However, the parallels among values for all three spacing values suggest that the models are generally reliable within the limits of the average gain test.

The three methods of finding gamma parameters differ in almost every category. The HW and TNL systems show various degrees of gamma-rod length increase as we increase the rod diameter, regardless of the spacing. The models show virtually no change in length within each of the spacing groups. The HW system shows a considerable increase in length as the rod diameter increases, while the increase is fairly modest for the TNL system. In all cases, the calculating methods show longer rods than the models. However, we cannot draw conclusions until we review the second part of this test series, using a different initial or pre-match feedpoint impedance.
The series capacitance values produced by each method present an equally befuddling array of differences within each method and between any two methods. The HW system produces only small changes in value across the span of rod diameters for wide-spacing values, but larger changes for narrow spacing values. The HW changes within spacing groups are in all cases smaller than for the TNL intra-group changes. The modeled values partially parallel the HW values in terms of the amount of change within each spacing group. However, the trends are not consistent between the calculating systems and the modeling system.
Before we rush to conclusions, we should repeat the very same tests using a different pre-match impedance. We shall retain every other beam detail, except that we shall use the version of the beam that shows a pre-match impedance of 29.84 - j25.73 Ohms. The results of this second survey appear in Table 3.

With respect to gamma rod length, within each group, the HW system shows an increasing length as we increase the rod diameter. Both the TNL system and the AM models show a decreasing rod length as we increase its diameter. Despite the different trends for the initial impedance of the antenna, the HW and TNL lengths are not very different from each other for any given element-to-rod spacing. However, the rod lengths required by the models are systematically longer. (This fact is exactly the reverse of what we saw when the beam's pre-match impedance was nearly resonant.)
With the high capacitive reactance of the pre-match impedance, the gamma-rod lengths remain relatively stable for all 3 methods within each increment of element-to-rod spacing. However, the series capacitance is another matter. The HW system shows the greatest rate of increase with increasing rod diameter, while the AM models show the smallest rate of increase. Both calculating systems produce much higher series capacitance values than the models, with the HW system showing values that are 100-150% too high. The TNL and AM series capacitance values are more closely--but not too closely--aligned.
The trends shown within each of the two test situations generally failed to parallel each other, despite the fact that the only difference between system inputs is the initial or pre-match impedance values. It would appear that we need a further type of test situation.
Test 3: Varying the Input Impedance
The goal of this test sequence is to determine--at least in a preliminary way--the effects of varying the pre-match feedpoint impedance, with special reference to the reactance. We already have sample of resonant and highly capacitively reactive impedances. We may use the same basic model of a 28-MHz 2-element Yagi and vary the driver length to create a reasonably fair sequence of reactance values. We need a positive limiting reactance value that is close to the negative limiting value. As well we need reactance values close to +/-13 Ohms as intermediate values between resonance and the limits. We can arrive at these values just by varying the length of the initial beam driver, as shown in the top section of Table 4. The resistive component of the pre-match feedpoint impedance will increase as the driver grows longer. However, the amount of increase should not be enough to invalidate this highly preliminary test sequence. We shall survey two gamma-rod diameters in order to assure ourselves that any trends are not mere quirks.

The lower portion of Table 4 shows the results of calculating the gamma parameters and of modeling them. Let's examine the results, separating the gamma length from the series capacitance, and also separating the two different gamma-rod diameters. Fig. 7 graphs the gamma-rod lengths for the 0.125" diameter gamma rod.

Both the HW and the TNL calculating systems show roughly equal rod lengths at the extremes of the test series, with the inductively reactive initial driver requiring a considerably longer length than the capacitively reactive driver by a factor of about 2:1. However, between these extremes, the two systems show curves with almost exactly opposite tendencies. Moreover, when we examine the modeled gamma-rod lengths, we find a quite different curve. The rod is shortest when the pre-match impedance is closest to resonance, with increases in length as the impedance becomes more reactive, regardless of the type of reactance.

When we increase rod diameter to 0.375", as shown in Fig. 8, the same tendencies repeat themselves, although the calculated lengths increase the ratio between the most inductive and the most capacitive reactance values. However, the modeled gamma-rod lengths show virtually the same values as shown in the curve for the 0.125" rod.
If we graph the series capacitance values for the 0.125" rod across the spread of pre-match impedances, the curves become quite interesting, as suggested by Fig. 9. Each method of reaching a capacitance value shows a peak, and the peak occurs at a different impedance for each method. The HW system arrives at a peak capacitance value at the intermediate capacitive reactance value, while the TNL system peaks at (or close to) resonance. The modeling method shows its peak near the intermediate inductive reactance value. We should remember that the model contains gamma end wires that are not a part of the calculating systems.

The capacitance curves for the 0.375" rod diameter show similar traits to those for the 0.125" rod. See Fig. 10. The calculating systems appear to show peaks with higher levels of reactance than we found to be the case for the thinner gamma rod. Once more, the TNL gamma matches show peak series capacitance values close to an initial resonant impedance, with the HW peak in the capacitive reactance region and the modeled match's peak in the inductively reactive region, relative to the initial or pre-match driver impedance.

Perhaps more vividly than any other test, the final series of tests shows one of the chief sources of differences among the three systems. The two calculating systems respond to differences in the feedpoint reactance in similar ways, although the length curves show opposite tendencies as the pre-match impedance approaches and passes resonance. If the test is representative, then we have established that the two systems are the same in principle, although they differ in detail. However, for changes in the gamma-rod length, neither system correlates well with the modeling method of designing a gamma assembly. Otherwise expressed, the modeling system of design fails to correlate well with the methods of calculation.
Note that I have emphasized the conditional nature of the test series. We have examined only the impedances that tend to apply to Yagi beams, that is, impedances below the feedpoint impedance. Establishing that the results are in fact representative would require a very large series of test sequences involving many possible impedance combinations relative to the feedpoint target and the pre-match values. At most, this test has established the importance of the pre-match impedance as a factor governing the results from each method.
Some Tentative Conclusions
I approached the gamma match out of curiosity. My inquisitiveness arose from the difference between series matching and beta matching calculation systems and the calculation of gamma matching systems. The first two methods produce precise results so that the most significant limitation when implementing one of them surrounds the physical properties of the components involved. For transmission line lengths, the accuracy of the velocity factor (or our ability to make linear measurements of the line) becomes the chief source of error.
The gamma matching system calculation methods show far less precise results. Some writers have ascribed most of the error to the lack of end wires in the calculated values. For many implementations, this convenient explanation seemed too weak to account for the differences. Therefore, I took two of the systems that are amenable to straightforward calculation progressions and compared their results to MININEC models using the most reliable version available of that software. The results of our preliminary series of tests--restricted to a 50-Ohm target feedpoint and to pre-match impedance values typical of Yagi arrays--show something else entirely.
The two calculation systems--HW and TNL--produce seemingly divergent results, especially with respect to variations among the main element diameter, the gamma rod diameter, and the spacing. However, if we employ a range of pre-match impedance values that vary mostly with respect to reactance, we begin to see an emerging pattern in which the calculated gamma lengths converge at high pre-match reactance values and diverge when the pre-match impedance approaches resonance. (We may bypass capacitance calculations, since they depend on the calculated gamma rod length.)
Perhaps the most disturbing aspect of the test series is the fact that neither calculation method approaches--either in values or in trends--what we find when we model a gamma match using MININEC models with nearly ideal AGT scores. However, we cannot in this case give automatic priority to the modeled results because they have not undergone confirming field tests. They simply serve here as a third method that differs in principle from the basic presumptions underlying the two calculation systems that we examined. Nevertheless, the differences in results among the methods strongly suggests that the present methods of calculating gamma match components fall seriously short of being precise.
We have had occasion to note that one point at which both the HW and TNL systems make a questionable assumption lies in the use of standard equations for calculating the transformed pre-match impedance to arrive at a value that we have called Z1. Remodeling the gamma to move the feedpoint to the main element at the junction of the gamma-half-element with the non-gamma-half-element suggests at least a phase shift and also significant variation from the calculated value of r that depends only on the physical properties of the assembly. The transformation also appears to relate to the pre-match impedance--especially the reactive component--although our test series is too small to reach two important conclusions. One conclusion would be the derivation of a revised step-up function, either as a correction factor on the usual calculation or as a substitute formulation. The other conclusion that we cannot draw is the adequacy of the modeled gammas to serve as source for such correctives.
Even if we could revise the available calculation systems, they would still fall short of the precision that we obtain from the calculations associated with series and beta matching systems. The methods by which we implement a gamma match include significant variables relative to even a precise calculation system. Fig. 11 shows some of the factors involved.

The upper portion of the sketch shows the general situation presumed by all of the methods that we have examined. The elements have a uniform diameter and thus most closely approximate sinusoidal current distribution. The end wires at the gamma far end and at the feedpoint have no weight in the calculation--except as post-facto fudge factors. Third, the series capacitance is precisely at the feedpoint of the gamma system.
The lower portion of the sketch shows some typical variations in the theoretical arrangement used in calculations. The elements in the HF range may use stepped-diameter structures that may vary the usual expectations for current distribution. The gamma rod normally extends beyond the shorting bar, leaving a small but definite radiating structure. The shorting bar at the gamma far end and the plate holding the coaxial cable connector have significant proportions that will vary from one installation to another. The sketch also shows the use of a tubular capacitor, a common HF technique to provide the series capacitance without concern for the voltage and current levels on the component and without concern for the effects of weathering. Once set, we may effectively seal the capacitor so that it requires only long-term maintenance. However, equally important to the type of capacitor used is its position. Typically, without regard to the type of capacitor used, gamma-match builders install the component on the gamma rod rather than at the actual feedpoint. Fig. 12 illustrates a sample of commercial gamma-match construction. By virtue of its position along the gamma line, the capacitor modifies both its influence on the feedpoint impedance and on the structure of the gamma line. As well, the physical implementation of the gamma must take into account any affects of the boom, if one chooses to connect the driven main element to the boom.

Therefore, even if we were to perfect gamma-matching system calculations, they would not yield the precision that we associate with other matching system calculations. Rather, they would serve only as a general guide to begin a process that only field adjustment can perfect. Indeed, for any selection of main element diameter, gamma rod diameter, and spacing between the two, there is a gamma length and a series capacitance that will effect a usable match to a desired main feedline over a wide range of pre-match impedance values--although not a completely unlimited range. As well, the gamma match will work either with or without a direct connection of the driven element to the boom.
Whatever the complexity of the calculation system, its output is simply a starting point to the process. We might as easily replace it with a table encompassing all of the successful implementations of gamma-match systems arranged by frequency, main element diameter, gamma rod diameter, and element-to-rod spacing (with annotations on the method of implementing the series capacitance). Such an archive--if it existed--would likely provide as much guidance to gamma-match dimensions as the current methods of designing them.
Updated 10-01-2006. © L. B. Cebik, W4RNL. This item first appeared in AntenneX, Sep., 2006. Data may be used for personal purposes, but may not be reproduced for publication in print or any other medium without permission of the author.