
 Some Notes on Two-Element Horizontal Phased Arrays
Some Notes on Two-Element Horizontal Phased ArraysWhen George Pritchard (ZL3MH, later ZL2OQ) introduced the amateur community to the 2-element phased array, it seemed to offer magic in the form of performance up to 7 dBd (9+ dBi free-space equivalent) and up to 40 dB front-to-back ratio. Unfortunately, the comparators of the day were relatively primitive 2- and 3-element Yagis that rarely performed up to their theoretical possibility. Nonetheless, the antenna type acquired the name "ZL-Special" and has been the subject of performance debate ever since. For a reasonably complete bibliography of ZL-Special articles in English, see my "Modeling and Understanding Small Beams: Part 5: The ZL Special," Communications Quarterly, (Winter, 1997), 72-90.
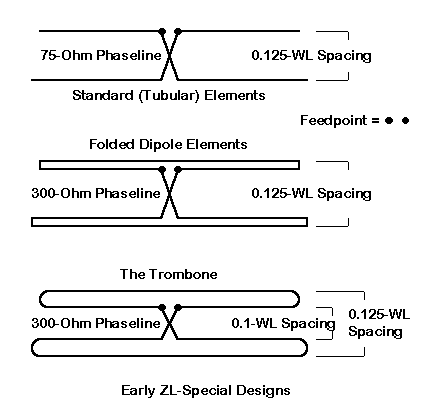
Fig. 1 shows several of the variations on the ZL-Special theme. Some of them work; others do not--or at least not very well. Virtually all early work on horizontal phased arrays presumed that we needed only attend to the impedance transformation along a transmission line. Hence, with 1/8 WL spacing and a similar transmission line, a half twist would yield a 135° phase shift with the accompanying high gain forward lobe and a deep rear null. Fig. 1 shows both linear and folded elements, along with the most popular phase line characteristic impedances. The trombone attempted to overcome the velocity factor of the common TV twinlead line (about 0.8) by making wide-spaced folded elements that were physically 1/8 WL at their outer edges but electrically 1/8 WL apart relative to the phase line. Although the trombone works quite well, the structure is completely unnecessary: simple folded dipoles would work as well.
Not until Roy Lewallen, W7EL, pointed out the fundamental error in amateur conceptions of the ZL-Special did we begin to re-analyze the 2-element horizontal phased array with some precision. (See Lewallen, "Try the 'FD Special' Antenna," QST (June, 1984), 21-24.) What controls the performance of the ZL-Special phase line is not so much the impedance transformation, but the current transformation (in terms of both current magnitude and phase angle). The current and the impedance do not change at the same rate except when the line is exactly matched to the element that forms its load. Hence, we had to take a wholly new approach to the single-line phased array. In these notes, we shall follow this lead.

Most radio amateurs do not fully appreciate how many variables are at work in this seemingly simple arrangement. First, the individual elements exhibit center-point impedances that are functions of the mutual coupling between them. The mutual coupling depends upon the element diameters, lengths, and spacing between them. Second, the feedline meets a parallel current division at the forward junction, which requires that all other variables result in the same voltage at the junction. The requisite voltage is a function of the source impedance of the forward element and the "share" of current received by that element.
Third, the rear element impedance at its center sets both a current magnitude and phase angle and a voltage magnitude and phase angle, both of which undergo transformation down the selected length of phase line. From Terman, Radio Engineers' Handbook (McGraw-Hill: 1943), p. 185, we have equations for the current and the voltage at any point down a transmission line from a load or antenna element. The following equations are for lossless lines, which is satisfactory for the short phasing lines used in 2-element horizontal phased arrays and which also coincides with the calculations within the TL facility of NEC-2 and NEC-4:
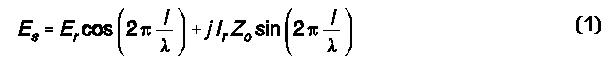

The meaning of the terms is as follows:
Because both the voltage and the current have an associated phase angle and resolve into real and imaginary components, the use of these equations in calculations is more complex that the initial appearance of them. Some of the math involved appears in the earlier note Communications Quarterly article. However, such calculations are available within NEC in the TL facility and are also available in the HAMCALC suite of GW Basic utility programs from VE3ERP.
Critical to our understanding of is the fact that the resultant values of voltage and current (magnitude and phase) at the forward end of the phase line are interactive, as the basic equations make evident. Achieving a current level that balances with the portion of source current used by the forward element at a common voltage such that the rear element then has a current magnitude and phase angle to yield a desirable pattern requires juggling all of the variables into a usable collection.
Even if we arrive at a usable collection of values, we have several other variables to consider. First, the calculated characteristic impedance of the phase line must be one that we can acquire or build. Second, the requisite physical length of the phase line (accounting for the line's velocity factor) for the current transformation must be at least the space between the elements. As well, it should not be too much longer than that spacing in light of practical considerations for supporting the line. Since the line will be open--whether we use coax or parallel line for the task--we must isolate it from disturbances that a metallic boom might create. Designing a ZL-Special, then, requires either careful analysis or some very lucky guesses.

Fig. 3 shows the 4 steps in our analysis, and the results appear in Table 1. If we arrange the elements individually in a NEC model and feed them independently with current sources, then the feed values in the table's step 1 under the relative current columns will result in the relative voltage and the individual element impedances. The models follow the system used in Part 1 of reversing the direction of the rear element relative to the forward element so that any phase line that we add can be in normal orientation. Notable is the similarity of the element impedances, a useful condition (but not the only such condition) for successful ZL- Special design. The tables in Part 1 show in a general way what conditions must exist for us to achieve such similar impedances: the relative longer length of the rear element when both elements are longer than a self-resonant dipole at the frequency of interest is a promising combination at the 1/8-WL spacing. As Fig. 4 shows, we have not striven for the highest gain or front-to-back value, but simply for highly usable values.

The second step in our analysis creates a model with a transmission line attached to the rear element, but with its forward end brought to a source wire independent of the forward element. The selected line--from calculations, is RG-83, 35-Ohms coax with a velocity factor of 0.66. The required length is 0.13 WL physically or 0.197 WL electrically. This length of the chosen line yields the correct relative rear element current magnitude and phase angle. At the same time, it yields the required forward-end voltage magnitude and phase angle to match the value for the forward element. Note that the required forward line end current is 0.664 (relative to a forward element value of 1.0) with a phase angle of 44.25°.
Step 3 in the analysis requires that we connect the forward end of the phase line and the forward element center to create a single feedpoint for the array. Under these conditions, supplying the feedpoint with a current of 1.0 at 0.0° phase angle, we obtain the relative element current levels and phase angles shown. The forward element phase angle is a function of the reactance at its center. However, the net phase angle difference between elements is still - 44.18°. At this stage, we have a complete array that we can frequency sweep from 28.0 to 29.0 MHz. Fig. 5 shows the results. The gain shows a nearly linear curve upward, with a total change of about 0.9 dB. The front-to-back ratio remains above 20 dB from the lower band edge to above 28.8 MHz and is at all points superior to the front-to-back ratio of a common reflector- driver Yagi by 5 dB minimum. However, as Table 1 shows, the source impedance is just above 20 Ohms.

The final step in our design is to add a matching system to raise the impedance to something compatible with common 50-Ohms coaxial cable. The low source impedance reactance suggest a matching section. A 0.13-WL section of the same 35-Ohms cable (RG-83) used for the phase line functions as a near-1/4-WL section to achieve the goal. With this section in place, we achieve the 50-Ohms SWR curve shown in Fig. 6. One might select other lengths for the matching line to better center the SWR curve, but the values shown would be in most cases quite satisfactory. For reference, Fig. 7 shows the array patterns at 28.1 and 28.9 MHz to confirm that the patterns are usable and to show the evolution of the rear lobes as we increase frequency.


The design explored here has attempted to show the required alignment of the many variables involved in ZL-Special design. It is not the only design that will work, but it shares many characteristic with successful ZL-Specials. Most significant is the required low characteristic impedance of the phase line, calling for a coaxial cable. Such lines are vulnerable to external disruption from near-metallic contact, so a non-conductive boom is desirable without resorting to complex phase line support construction.
Sample ZL-Special Analysis Data
The following data come from NEC-2/NEC-4 models of a 2-element horizontal phased array for
28.5 MHz using 0.5" aluminum elements. The rear element is 0.506 WL long, while the forward
element is 0.465 WL long. The modeling environment is free space. In all cases, the free-space
gain is 6.34 dBi, and the 180° front-to-back ratio is 30.15 dB.
Step 1. Independent elements, independent sources:
Element Rel. I Rel. I Rel. V Rel. V Impedance
magnitude phase angle magnitude phase angle R +/- J X Ohms
Rear 0.8935 -44.18° 26.24 -23.58° 27.49 + j 10.34
Forward 1.0 0.0° 33.53 31.94° 28.46 + j 17.76
Step 2. Independent elements, independent sources, phase line installed:
Element Rel. I Rel. I Rel. V Rel. V Impedance
Magnitude phase angle Magnitude phase angle R +/- J X Ohms
Rear 0.8935 -44.15° --- --- 27.49 + j 10.34
Phaseline 0.664 44.25 33.56 32.02° 49.74 - j 8.98
Forward 1.0 0.0° 33.51 31.96° 28.43 + j 17.73
Step 3. Phase line connected to forward element, single source
Element Rel. I Rel. I Rel. V Rel. V Impedance
Magnitude phase angle Magnitude phase angle R +/- J X Ohms
Rear 0.5734 -60.80° --- ---
Forward 0.6418 -16.62° --- ---
Feedpoint 1.0 0.0° 21.53 15.34° 20.76 + j 5.70
Step 4. Matching section added:
Element Rel. I Rel. I Rel. V Rel. V Impedance
Magnitude phase angle Magnitude phase angle R +/- J X Ohms
Rear 0.9774 -133.7° --- ---
Forward 1.0939 -89.48° --- ---
Feedpoint 1.0 0.0° 60.67 6.14° 60.32 + j 6.49
Table 1. Sample ZL-Special analysis data from NEC models in the 4 steps of antenna analysis
demonstrated in the text.

W7EL's "Field-Day Special" rests on a different approach--an attempt to calculate the mutual impedance consequences of the elements, with the selection of element length, spacing, and line length designed to achieve the required current magnitude and phase angle transformation. Fig. 8 shows the outline of a 10-meter version of the antenna that I have built. The line lengths indicated are for modeled versions using #18 wire at a 1" spacing (about 450 Ohms impedance as a transmission line and for #20 wire spaced 0.375" (about 300 Ohms as a transmission line. The longer length for the thinner wire, when taken individually and as a spaced 2-wire pair) is natural. The following notes are based on the 1"-spaced model. In both cases, using vinyl-covered wire shortens the physical element by 1-2% to account for the velocity factor of the insulation in antenna use.

Although the element spacing is 4.27' (0.1237 WL), the phase line is 4.9' (0.1420 WL) long, despite the 0.8 velocity factor of high-quality twinlead. Indeed, calculations suggest that a higher front-to-back ratio results from the use of 340-Ohms line. However, as Fig. 9 shows in the free-space azimuth patterns across the first MHz of 10 meters, performance with a 300- Ohms line achieves similar levels to the first design that we explored. As well, with a 300-Ohms line, slightly better performance is possible by lengthening the forward element slightly, although the difference is unlikely to be noted in practical operation.

Fig. 10 shows the gain and 180° front-to-back curves for the model across the 28.0 to 29.0 MHz span. Typical of ZL-Special designs of any sort, the gain rises almost linearly, while the front-to-back ratio shows a broad peak centered a bit below the center of the design passband. Fig. 11 provides figures on the resistance and reactance within the design passband. The resistance range is only about 7.5 Ohms. The reactance changes by a total of 56 Ohms. As Fig. 8 indicated, a pair of series capacitors, each with a reactance of -110 Ohms (about 50 pf at 28.5 MHz) would provide a very reasonable SWR curve across the passband.

The need for a compact portable antenna inspired the original design of the Field-Day Special. However, for our purposes, it serves additional functions. One is to illustrate that equal- length elements (each about 0.468 WL long) result in wide-band performance that is not significantly different from the use of unequal length elements in the first example. A second function is to show that folded dipole elements have no advantage or disadvantage relative to single elements in performance--although there may be differences in the physical convenience of one or another element type. Third, the elements have widely divergent impedances: forward Z 124 + j 84 Ohms; rear 80 - j 256 Ohms. Nevertheless, the right length of the right impedance phase line effects the correct current division at the feedpoint junction so that we arrive ar the correct current magnitude and phase angle on the rear element to achieve proper or acceptable phased performance.

The design uses the same element lengths as our initial model. The forward element is 0.465 WL long and the rear element is 0.506 WL long. Both are 0.5" (0.001207 WL) diameter aluminum. The original design used a single phase line length of 0.13 WL of 35-Ohms 0.66 velocity factor line. Suppose that one cannot obtain the required RG-83, but has some RG-8X with a 50-Ohms impedance and a velocity factor of 0.78. The higher-impedance line at any length will not achieve in a single line the desired phasing for reasonable ZL-Special performance.
However, we may effect transformations of current magnitude and phase angle on both the forward and the rear elements by bringing lengths of transmission line from each element to a middle point. The length of line from the rear element is 0.13 WL. Although this length is physically similar to our original design, electrically, it is only 0.167 WL electrically, since the velocity factor of our new line is higher. A 0.015-WL line from the forward element is 0.192 WL electrically or about 0.52'. At the junction, given a source current of 1.0 at 0.0°, we arrive at a relative current split of this dimensions: forward 0.950 at 4.35° and rearward 0.458 at -2.1°. The resulting current ratio of rear to forward elements is 0.811 at -44.8°, close to the values for the original design.

Fig. 13 shows the azimuth patterns across the 28-29 MHz span of the design passband. Only the front-to-back ratio suffers a bit relative to the more ideally phased original example, as shown in the gain and front-to-back curves in Fig. 14. A bit of element length adjustment might well have improved the numbers a bit, but would have altered the demonstration.

The natural impedance at 28.5 MHz for the new phase line arrangement is about 23.5 + j 13.1 Ohms. The low reactance suggests that a modified 1/4-WL line section might effect a match. 0.167 WL (electrical) of 35 to 37 Ohms line provides the broad 50-Ohms SWR curve shown in Fig. 15. The line might consist of either RG-83, or in the absence of such line, a parallel section of RG-59. In each case, the line velocity factor will determine the physical length.

The design shown here is similar in principle to the one used to improve front-to-back performance of a 10-meter hilltopper 2-element Yagi. (See "Two Hilltoppers for 10 Meters," The ARRL Antenna Compendium, Vol. 6, pp. 1-9.) Like the single-line ZL-Special, the antenna requires a non-conductive boom to ensure that the phase-line remains clear of unwanted interactions.
Many possible ZL-Special designs prove to be unfeasible. The requisite characteristic impedance of the phasing line may not exist and cannot be constructed. The required line length may be shorter than the distance between the elements, or it may be excessively long.
The key to successful ZL-Special design is to find a set of element lengths and a spacing that meets two conditions. First, the relative current magnitude and phase angle on the individual elements must provide a satisfactory pattern in terms of gain and front-to-back ratio. Second, the impedances of the elements under the first condition must permit the design of a phasing line (or pair of lines) that employs an available or achievable characteristic impedance and that allows the requisite current division and transformation. As we saw in Part 1, there is in principle not restriction upon element spacing within the range of 0.05 to 0.2 WL, although element spacing in the 0.1 to 0.13 WL range tends to yield the most easily achieved gain and operating bandwidth levels.
There is, in principle, no restriction upon the element lengths relative to the length of a resonant dipole at the design frequency. As well, there is no restriction upon the relative lengths of the elements: the forward element may be in principle shorter than, equal to, or longer than the rear element. Some combinations may be more favorable than others, although to date, there is no complete survey of all combinations.
Perhaps the major disadvantage of the ZL-Special phasing system lies in the need to use folded dipole elements with high-impedance phase lines or to use with single tubular elements a low-impedance line. Many, if not most, builders wish to use a metallic boom and hence to have a phase line that is not susceptible to unwanted interactions. The quest for a stable phasing system has led to some interesting variants of phasing schemes for the 2-element horizontal array. The early HB9CV system--still in use today--and the recent N7CL system are two approaches to the same end. If the elements and the desired phase line do not match, let's add matching networks. As we shall see in the next episode, a slight increase in electrical complexity can lead to significant simplifications in the physical design of 2-element horizontal phased arrays.
Updated 03-14-2002. © L. B. Cebik, W4RNL. This item originally appeared in The National Contest Journal (Mar/Apr, 2002). Data may be used for personal purposes, but may not be reproduced for publication in print or any other medium without permission of the author.