
 Circularly Polarized Aimed Satellite Antennas
Circularly Polarized Aimed Satellite AntennasAmong aimable satellite antennas, we generally have two options. The axial-mode helical antenna has become a favorite among some satellite and other operators, especially at UHF (435 MHz and up). However, the crossed and turnstiled Yagi remains in favor among other operators. Let's explore these options, at least to a small extent, on common ground.
The Axial-Mode Helical Antenna
The following notes on axial-mode helices summarize parts of my longer study, "Notes on Axial-Mode Helical Antennas in Amateur Service," which appeared in the 2005 Proceedings of the Southeastern VHF Society. There I examined NEC-4 models of 5-, 10-, and 15-turn helices both over perfect ground and over ground-plane wire-grid screens. Figure 1 shows the general outline of the models, as well as their relative sizes, using a 1.2-wavelengh-by-1.2-wavelengh screen that is 1-wavelengh above ground. The test frequency is 299.7925 MHz, where 1 meter = 1-wavelengh. You may scale the designs for other frequencies by using the ratio of 300 to the new frequency times each of the critical dimensions, including the wire diameter but excluding the pitch angle. For uniformity, all models point straight up.

The need for such a study is a function of the classical literature on axial-mode helices. Researchers tend to treat the antenna as a broadband array, and extrapolating data useful to amateur spot-frequency use is somewhat daunting. (See the final notes for some references, especially VE3NPC's more recent empirical measurements.) Modeling this type of antenna also requires considerable care.
Perhaps the two most critical dimensions are the pitch angle and the circumference. In fact, basic helix theory tends to restrict axial-mode operation of the helix to pitch angles between 12° and 14°. The smaller the pitch angle (within limits), the higher will be the gain of a helix with a fixed number of turns. As well, various texts restrict the circumference to ranges from either 0.8-wavelengh to 1.2-wavelengh (Kraus) or from 3/4-wavelengh to 4/3-wavelengh (Balanis). The number of turns in a helix is a builder selection, as gain (for any given pitch and circumference) rises with the number of turns. As well, selection of a wire diameter is also a builder choice. Although not mentioned in any serious way in most literature, conductor size does make a difference to helix performance. The larger the wire diameter as a fraction of a wavelength, the higher the gain for an otherwise fixed helix size. The sample models that we shall explore use 2-mm diameter wire.
There are two major issues with modeling an axial-mode helix. The first issue arises from the fact that NEC must use straight wires to simulate a circle. The difference between the circumference of a circle and that of a polygon inscribed within the circle only reaches relative insignificance as the number of sides on the polygon passes about 16 or so. A 16-sided regular polygon inscribed within a circle has a circumference that is about 99.4% that of the circle. For a more rounded number in my NEC-4 helix models, I used 20 segments per turn. Using 2-mm diameter wire, the segment length-to-radius ratio remained well above modeling minimums.
The second major issue involves the reported vs. the actual gain of the helix models. For both the perfect-ground and the wire-grid-plane models, I assigned the source to the first segment, the one in contact with the ground surface. Because this segment does not have equal length wire segments on either side of the source segment, the initial reports of gain and source resistance will be erroneous but correctable. By moving the source segment to other segments, I ascertained that applying standard Average Gain Test (AGT) adjustments to the gain values would yield very reasonable corrected reports.

Figure 2 shows the results of gradually increasing the circumference of 5-, 10-, and 15-turn helices (12° pitch, 2-mm diameter wire) over wire-grid planes that are 1.2-wavelengh on a side and 1-wavelengh above average ground. The gain curves are similar to those produced by the NEC-2 models created by Paolo Antoniazzi, IW2ACD, and Marco Arecco, IK2WAQ, in "Measuring 2.4 GHz Helix Antennas," QEX, May/June, 2004. The major difference is that the ground beneath the helix in my models yields a moderate rise in gain below the generally accepted optimal circumference range. Both sets of curves show that as the helix grows longer, the optimum circumference for maximum gain decreases. Exceeding the optimal circumference results in a steep loss of gain potential. With a constant pitch angle (12°), the peak-gain circumference decreases by about 0.05 wavelength with each 5-turn increase in helix length.

The dimensions for 3 sample axial-mode helical directive arrays appear in Table 1. The arrays correspond to 12° pitch 5, 10, and 15 turn antennas at 299.7925 MHz, where 1 m = 1 wavelength. The modeled performance data appears in Table 2. The gain values have been corrected for the average gain test (AGT) score, and raw reports will be somewhat lower. The peak gain of the helices is about 11.7, 13.0, and 14.2 dBi for the 5-, 10-, and 15-turn antennas, respectively. Note that the gain increases almost linearly with the increase in the number of turns. This fact is important to keep in mind when comparing axial-mode helices with alternatives to them as circularly (or nearly circularly) polarized antennas.

Modeling the helix itself is simplified by the GH entry in NEC. However, the NEC-2 and the NEC-4 versions of that geometry command differ radically. Therefore, modelers need to consult the appropriate manual for guidance. (The commands are available in NEC-Win Pro and in GNEC, by Nittany-Scientific, with entry-formation assistance screens.) An alternative method of creating a helix appears in EZNEC Pro, which allows helix creation as a set of individual wires batch created by entries similar to those used in the GH command. The termination of the helix on perfect ground is simple enough, but mating the lowest wire end to a wire-grid junction may call for the modeler to displace the wire end to meet the closest junction. The size of the elevated ground-plane surface for a given helix does make a difference in the performance of the antenna, although gain changes are small. There is an optimal size that varies with the length of the helix. The ground screens in the sample models are close to optimal.

An axial-mode helical antenna rarely yields perfect circular polarization. Instead, it yields elliptical polarization with a major and a minor axis and a tilt angle. The antennas approach perfect circularity most closely along the axis of the helix. Applications needing something closer to circular perfection tend to work with quadrifilar designs, although they are impractical for amateur satellite service. The sample models improve their circularity with increased length. More pertinent to amateur use is the fact that an axial-mode helix does not produce a perfect single-lobe pattern. Figure 3 shows the total field patterns of the 5-, 10-, and 15-turn helices over an elevated ground screen. In each case, we can see a considerable collection of side lobes. Each model uses the circumference that produces the best gain, but that circumference does not yield the lowest level of side lobes. Reducing the circumference produces lower gain (from 1 to 2 dB, depending upon the length of the helix), but results in a cleaner pattern. Circumferences below about 0.85 wavelength rarely have any sidelobes at all through the 15-turn limit to my investigation.

As well, there are remnants of opposite-direction polarization within the total field of the axial-mode helix. Figure 4 shows the dominant right-hand polarized component of a 15-turn helix over a ground-screen elevated above average ground. The left-hand component is down by 25 dB, with some of the lower lobes being composed mainly of left-hand components. All of these facets of axial-mode helix performance have a bearing on the sensitivity of such antennas to off-axis signals, whether at high or low angles relative to the axis that marks the centerline of the helix. How much side-lobe and oppositely polarized lobe suppression is enough, of course, is a user determination based upon the application and the local circumstances of use.
These notes have not addressed the question of constructing a helical antenna. Chapter 19 of The ARRL Antenna Book provides some of the general schemes used. For UHF, the most common technique is to use a non-conductive central shaft with periodic side-projections to support the helix turns at critical points. (Fowler also uses a conductive center support rod with no degradation of performance.) The number of supports per turn depends upon numerous factors, including the inherent stiffness of the wire or tubing used to form the helix. A central shaft has a mechanical advantage by allowing attachment to the ground-plane screen, cup, or grid. Hence, the wire turns do not experience much stress, except for the inevitable attachment to a connector. Standard references give the impedance as 140 times the helix circumference in wavelengths. However, the impedance will vary with the helix structure at the terminating end and with the diameter in wavelengths of the element wire. As the impedance varies, so too will the matching method selected for use with the coaxial cable. In such applications, the coax used for the main feedline may be 50 Ohms or (for those using surplus solid sheath varieties) 75 Ohms.
The dimensions for an axial-mode helical array are implicit in the set of design criteria to which we build. Hence, I have given only overall dimensions, although you may easily derive more specific dimensions from the graphs shown and the basic trigonometry for the design work. The following dimensions--many of which are inter-dependent--define a helix.
R = radius of the helix, wire-center to wire-center C = circumference of the helix C = 2 p R S = spacing between turns S = C tana a = pitch angle a = tan-1 (S/C) N (or n) = number of turns L = axial length of helix L = n S D = conductor diameter L' = conductor length for a single turn L' = SQRT(C2 + S2) = C/cosa = S/sina
All dimensions refer to center-to-center distances relative to the wires. The last two items in the list are relevant to the physical planning of the helix design.
If these notes give the impression that the axial-mode helix is somewhat imperfect, the impression is correct. However, it is not so far from perfect to bar its effective use in satellite applications. The antenna originated as a broadband array and has been pressed--sometimes uncritically--into spot frequency or narrow-band uses. Understanding the fundamental properties of axial-mode helices in this context is an essential ingredient to producing an antenna that fulfills its promise to the limits of its ability.
Alternative Parasitic Arrays
An alternative to the axial-mode helical array is a parasitic array with turnstiled or quadrature fed drivers. Up to a point--but not necessarily beyond that point--such arrays offer some advantages over helical arrays. Not the least of these advantages is our familiarity with the construction techniques involved in building them and matching them to standard coaxial cable feedlines.
Unlike the helix and its design equations, most parasitic arrays are designed by model or experiment--or both--for a certain level of performance at a given frequency within some overall size constraint. Therefore, we shall offer some dimension tables for our samples without in the least claiming them as the best possible designs. The goal will be to note some significant differences between parasitic and helical arrays designed for circular polarization. The design models are for 299.7925 MHz to coincide with the helix designs that we have so briefly surveyed. Like the helices, the parasitic arrays can be scaled to other frequencies.
When most folks think of parasitic arrays with circular polarization (or an approximation thereof), the crossed Yagi comes to mind. Although that antenna is certainly one of our alternatives, it is not the only one. Neglected is the quad beam, which one may convert to circular polarization without adding any further elements beyond those needed for ordinary or linear polarization.

Figure 5 shows 3 of our samples to illustrate their comparative sizes. For moderate gain levels, the parasitic arrays have boom lengths that are much shorter than corresponding helical arrays. For example, a 10-turn helix with a gain of about 13 dBi is almost a half wavelength longer than a 10-element Yagi with about a half-dB higher gain. However, we have noted that helices tend to increase in gain almost (but not quite) linearly with added turns, while adding more directors to a parasitic array results in a decreasing gain-per-new-element value. Hence, there is a crossing point at which the helix may show more gain than a parasitic array of the same overall length. That crossover point most likely occurs when the arrays approach 5 wavelength in overall length.

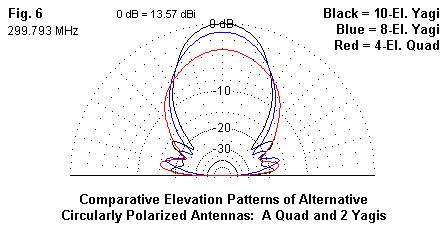
The first non-helical candidate is a 4-element quad, the dimensions for which appear in Table 3. The quad is only 0.91 wavelength long from reflector to the forward-most director. Using 1-mm diameter wire for the elements, it has a gain of 10.6 dBi when placed 1 wavelength above average ground. The quad's beamwidth is 58°. The performance of the quad is more completely summarized in Table 5, along with the other sample candidates as alternatives to the helix. Two sets of values are especially significant. One is the high value of front-to-sidelobe ratio (listed as a negative value of dB below the main lobe gain value), when compared to the much smaller ratio shown by the helices. In fact, Figure 6 shows the elevation patterns for the quad overlaid with two of the Yagis for direct comparison with the helix patterns shown in Figure 3.
Because a quad allows some flexibility in the placement of the driver without undue adverse effects on the array gain, we may arrive at a single-source impedance of about 95 Ohms resistive. Hence, a 1/4 wavelength section of 93-Ohm cable forms a proper phase line run between successive corners of the driver. The result is a circularly polarized antenna. This technique first came to my attention in a sample model that Brian Beezley, K6STI, included in the model collection that accompanies his AO program. We should not run the phase-line coax parallel to the active element. Hence, it is likely that we would use a 3/4 wavelength section of line running from one corner to the center non-conductive boom and back to the adjacent corner. We may reverse the polarization simply by connecting the main feedline at one or the other end of the phase line. Higher isolation feeding methods have appeared from time to time. For this simple system, the result is a 50-Ohm impedance for the main feedline. The 4-element quad in the outline sketch has a 2:1 50-Ohm SWR bandwidth of more than 25 MHz, which eases the problems associated with construction variables. (Redesigning the antenna for fatter elements would yield a larger bandwidth.) Obviously, longer versions are possible for the quad if one desires more gain. However, in our survey of alternatives, let's turn to some Yagi designs.

Table 4 provides the dimensions of 3 sample Yagis, all derived indirectly from normal Yagis of DL6WU vintage. The short 8-element version is 1.42 wavelengths long, while the 10-element version has a boomlength of 2.05 wavelengths. The 12-element version is 2.60 wavelengths long. The last sample Yagi appears mostly to demonstrate that as we add new directors, the increase in gain dwindles per added element. Nevertheless, the 14.2-dBi gain of the 12-element Yagi compares well to the peak gain of the 15-turn helical antenna with a total length of over 3.6 wavelengths.
Since NEC uses only axial currents in calculating the antenna fields, one may model crossed Yagis with each crossed parasitic element pair joined at the center. If there are any interactions, they will not show in the model. In practice, it is likely that one will use a pair of independent linear elements. Since the drivers require separation, if only by a small distance, to establish their independence, it will not harm construction to use the same separation between parasitic elements. The modeled dimensions in Table 4 presume the use of a non-conductive boom.

Table 5 summarizes the potential performance of the Yagis. The total field patterns for the 8- and 10-element versions appear in Figure 6, along with the quad. I omitted the 12-element Yagi lest the morass of pattern lines become unreadable. Each Yagi shows close to the same front-to-sidelobe ratio--about 15-16 dB. As well, all of the Yagis show the same high ratio of right-hand gain to left-hand gain. Figure 7 shows the polarized components of the 10-element Yagi for illustration of the difference. You may wish to compare this pattern with Figure 4, the comparable pattern for a 15-turn helical design.

All of the Yagis use identical feed systems to establish quadrature and a match to a 50-Ohm feedline. In this particular design, the single driver source impedance is 50 Ohms. Hence, the turnstile phase-line is also 50 Ohm. The resulting impedance presented to the main feedline is close to 25 Ohms. A length of 35-Ohm line (or a pair of 70-Ohm lines in parallel) provides the required match for a 50-Ohm main feedline. As with the quad, one may change polarization simply by swapping phase-line ends for the junction with the matching section and main feedline. Removing the phase-line altogether converts the array to linear polarization, with the un-fed elements having little if any effect on operation in this mode.
To center the design frequency within the overall 2:1 50-Ohm SWR passband, the line lengths for both the phase line and the matching line are not true quarter wavelengths electrically. The electrical length of the phase-line is a bit over 0.22 wavelength, while the matching line is close to 0.215 wavelength. The 2:1 SWR passband, as illustrated in Figure 8, runs between 270 and 330 MHz, a 60-MHz spread that should make home construction less critical. However, as with any antenna based upon turnstiled dipoles, the SWR bandwidth will be far wider than the operating bandwidth for which the patterns hold their desired shape. Hence, it remains good design practice to optimize the performance of the crossed Yagis for the desired range of operation. An SWR meter alone is not sufficient to optimize any circularly polarized antenna.

The physical implementation of a parasitic design will require considerable effort. Never assume, but actually measure the actual velocity factors of the lines. Construction will require close attention to line dress and to the potential effects of any connector installed. For UHF and upward, one should use certified connectors rather than hamfest specials and bargains. Even the solder lumps that close the wire loops of the quads can create detuning effects from 70 cm upwards. Whether you are building a helix or a Yagi, the casual and careless construction techniques that are harmless at HF become potential plagues to UHF antennas.
Conclusion
As always, we have looked at alternatives for antennas meeting a certain set of needs. In this case, we selected satellite communications, with its need for circular polarization--or as closely as we may approximate circular polarization using standard construction techniques. The key alternatives for antennas that we steer with respect to both azimuth and elevation are axial-mode helical arrays and turnstiled parasitic arrays.
Both techniques will produce able arrays. Our survey and samples do not exhaust the designs that we may bring to bear on the communications need. However, they should open the door to relevant considerations in making a choice between the two major routes to circularly polarized antennas and to some of the considerations when designing an antenna within either general category.
Reference Note
There are a number of background sources for information on axial-mode helices. The following list is a start, with most of the items having extensive bibliographies. John D. Kraus, Antennas, 2nd Ed. (1988), pp. 300-310.
H. E. King and J. L. Wong, "Helical Antennas," Chapter 13 of Antenna Engineering Handbook, 3rd Ed., R. L. Johnson, Ed. (1993), pp. 13-1 ff.
Darrel Emerson, AA4FV, "The Gain of an Axial-Mode Helix Antenna," The ARRL Antenna Compendium, Vol. 4 (1995), pp. 64-68.
C. A. Balanis, Antenna Theory, 2nd Ed. (1997), pp. 505-512.
W. L. Stutzman and G. A. Thiele, Antenna Theory and Design, 2nd Ed. (1998), pp. 231-239.
Paolo Antoniazzi, IW2ACD, and Marco Arecco, IK2WAQ, "Measuring 2.4 GHz Helix Antennas," QEX, May/June, 2004, pp. 14-22.
L. B. Cebik, W4RNL, "Notes on Axial-Mode Helical Antennas in Amateur Service," Proceedings of the 2005 Southeastern VHF Society Meeting, pp. 82-121.
Clare Fowler, VE3NPC, "Real World Helix Antenna Measurements," The AMSAT Journal, May/Jun, 2006
Also see the Antenna Modeling Programs page for more information.
Updated 08-27-2007. © L. B. Cebik, W4RNL. This item first appeared in QEX, Sep/Oct, 2007, pp. 51-56. Reproduced with permission. Copyright ARRL (2007), all rights reserved. This material originally appeared in QEX: Forum for Communications Experimenters (www.arrl.org/qex).